암호화폐의 암호학 : ECDSA 와 RSA

1. 본인인증이 필요한 이유

우리가 카드를 이용해 5만원 이상을 결제하거나, 여권이나 통장을 새로 발급받거나, 뭔가 내 돈이 아닌 돈을 사용하고 영수증을 제출할 때는 항상 우리의 서명(Signature)을 필요로 한다. 혹자는 이 서명을 중요하지 않다고 생각할 수도 있지만, 서명은 본인이 맞음을 증명하데 꼭 필요한 요소다.

신용카드를 잃어버렸을 때 다른 사람이 내 카드로 결제했다면, 이 결제가 내가한 것이 아니라는 걸 증명해야 할 때 특히 서명은 중요한 역할을 한다. 우리나라의 경우 1993년 금융실명제가 발효되며 신분증 등을 통해 본인임을 증명해야하고, 간편결제를 할 때도 Face ID나 PIN 등 본인 확인 절차가 반드시 요구된다. 전자상거래가 활발하게 이루어지는 지금, 해당 거래가 본인이 했음을 증명하는 본인인증은 절대로 빠질 수 없는 요소이다.

암호화폐 역시 마찬가지이다. 내가 어떤 암호화폐를 소유하고 있음을 증명해야 할때, 누군가에게 송금하는 거래가 발생할 때 본인확인을 할 수 있는 디지털 서명(Digital Signature)이 필요하다.

이때 디지털 서명은

암호화폐에서 많이 사용되는 디지털 서명 방식은 ECDSA(Elliptic Curve Digital Signature Algorithm; 타원곡선 디지털 서명 알고리즘)와 RSA(Rivest Shamir Adleman) Algorithm 두 가지가 있다.

2. 디지털 서명 알고리즘, ECDSA와 RSA

ECDSA와 RSA, 어떻게 작동하나

나의 서명은 나만 만들 수 있어야 한다. 나만의 필체를 이용한 그림이 될 수도 있고, 내가 가진 하나 뿐인 도장으로 새긴 무늬, 혹은 나만 갖고 있는 열쇠(Key)로 만든 암호가 될 수도 있다. 그 중에서도 디지털 서명은 자신의 암호키를 가지고 특정한 정보를 암호화시키는 방식으로 만들어진다. 디지털 서명 방식에 필요한 열쇠는 암호화가 가능한 개인키(Private Key)와 복호화가 가능한 공개키(Public Key) 두 가지가 있다.

ECDSA와 RSA 모두 비대칭 알고리즘(Asymmetric Algorithm)이다. 예를 들어보자. 보물이 가득 담긴 보물 상자를 여는 열쇠는 상자를 잠글 때도 쓸 수 있고, 잠긴 상자를 열 때도 쓸 수 있다. 이렇게 똑같은 열쇠(Key)를 가지고 암호화(encoding)과 복호화(decoding) 모두 가능한 암호화 방식을 대칭 알고리즘(Symmetric Algorithm)이라고 한다. 하지만 만약 철수가 가진 열쇠는 상자를 잠그는 것만 가능하고 (개인키), 반대로 영희가 갖고 있는 열쇠는 잠긴 상자를 여는 것만 가능하다면 (공개키), 이런 암호화 방식은 비대칭 알고리즘이라고 부른다.

대신 ECDSA와 RSA는 각각의 열쇠를 생성하는 방식에 차이가 있다. 그리고 둘 중 무엇이 더 나은 서명 방식인가에 대해서는 여전히 논쟁 중이다. 가장 잘 알려진 암호화폐인 비트코인(BTC)과 이더리움(ETH)은 ECDSA의 secp256k1 curve를 이용해 열쇠를 생성한다. RSA는 1977년 창안된 비교적 오래된 방식으로, 서명을 검증(verify)하는데 걸리는 시간이 ECDSA보다 짧다. 하지만 서명의 크기가 크고 생성 시간이 더 길다는 단점이 존재한다. 왜 이런 차이가 나는지 알아보기 위해, 지금부터 두 서명 알고리즘의 작동 방식을 알아보자.

RSA Algorithm

RSA Algorithm이 가장 유명한 비대칭 암호화 알고리즘임이라는 사실은 두말하면 잔소리다. SSL/TLS 인증서, 각종 암호화폐를 비롯해 이메일 암호화 등 도처에 사용된다. 전하고자 하는 데이터(주로 text)를 단방향 암호화시키기 위해 소인수분해(Prime Factorization)를 이용한다. 엥? 우리가 중학생 때 배운 그 소인수분해가 맞다. 이 방식은 무작위로 거대한 두 소수(素數; Prime number)를 선택하고, 이 두 소수를 곱해 하나의 아주 아주 큰 수를 만드는 것이다.

두 소수를 곱해 하나의 큰 수를 만드는 연산은 비교적 간단하다. 단순 곱셈을 한 번만 하면 된다! 물론 수가 클수록 연산이 오래 걸리겠지만, 그 시간은 자릿수에 대해 선형적으로 증가할 것이다. 이것도 오래 걸리지 않느냐고? 그렇다면 반대로 곱해진 큰 수를 소인수분해해서 원래의 두 소수를 찾는데는 시간이 얼마나 걸릴까? 그 거대한 수를 2부터 시작해서 나누어지는지 전부 확인하는데 걸리는 시간은, 숫자가 커질수록 매우 가파르게 증가한다. 시간복잡도에 대해 이해하고 있는 사람이라면 기하급수적(exponential)으로 시간이 늘어난다는 걸 알 수 있을 것이다. 그래서 양자 컴퓨터가 아닌 현대의 슈퍼 컴퓨터로 사실상 불가능(virtually impossible)한 과제로 분류된다. 768자리 수를 소인수분해하는데 걸리는 시간은 컴퓨터 80대를 사용하면 1500년 정도 걸린다는 연구 결과가 있다(논문).

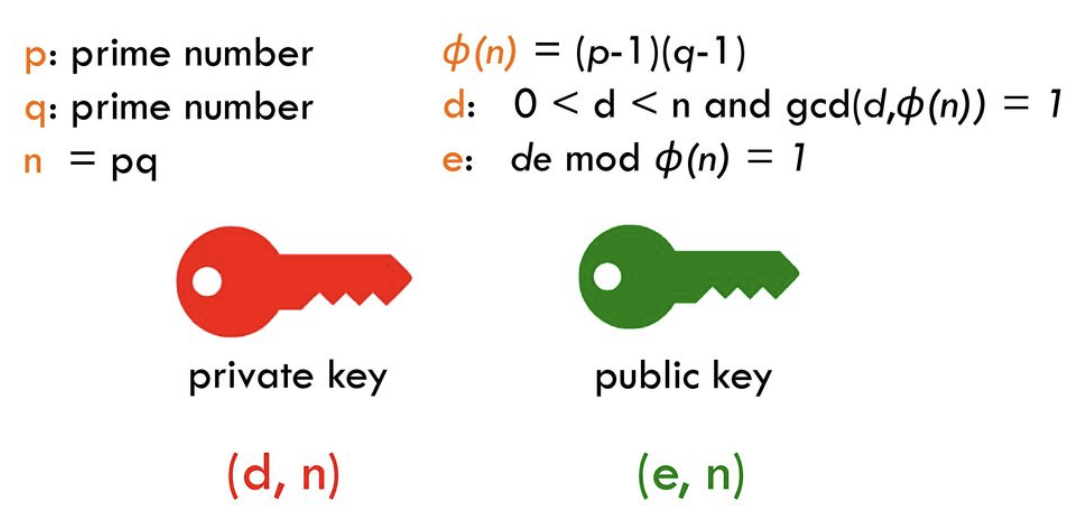
보안성이 높다는 장점 덕분에, 이 방식이 표준화된 1994년 이래로 근 30년 간 수많은 곳의 디지털 서명, 혹은 암호화 알고리즘으로 널리 채택되고 있다. 비교적 최근에 나온 타원곡선 알고리즘과 비교해도 될만큼 RSA는 오랜 기간 입지를 유지하고 있다. 잘 만들어진 것도 있지만, RSA는 여타 다른 알고리즘에 비해 매우 간단하다(아마 ECDSA를 보면 그렇게 생각할 것이다). 간단한 수학적인 아이디어를 발전시켜 공개키(Public Key)와 비밀키(Private Key)를 만들 수 있다.

ECDSA, 타원곡선 디지털 서명 알고리즘

ECDSA(Elliptic Curve Digital Signature Algorithm), 또는 ECC(Elliptic Curve Cryptography)는 한국어로 타원곡선 전자서명, 타원곡선 암호화라고도 불린다. 아마 암호학에 관심이 있다면 한 번쯤은 들어봤을 것이다. DSA(Digital Signature Algorithm)를 계승해서 만들어진 이 알고리즘의 개념은 1980년도에 제안되었지만, 실제로 이 개념의 구현은 2005년이 되어서야 이루어졌다.

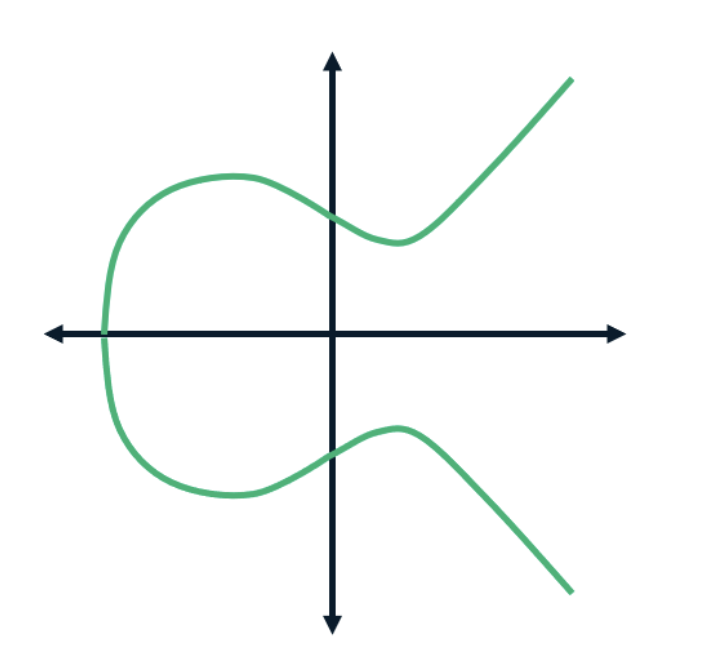
위 그림같은 타원곡선 상의 한 점으로 대응시키는 함수를 이용해 원하는 정보를 암호화한다. 이때 대응시키는 함수는 X → Y 방향으로의 계산은 쉽지만, Y → X 방향으로의 역연산은 어려운 함수를 사용하는데, 이런 함수를 트랩도어 함수(Trapdoor Function)라고 한다. 트랩도어 함수는 Y → X 방향의 역연산이 어렵지만, 만약 Trapdoor라는 추가적인 정보를 알고 있으면 역연산이 쉬워진다.

ECDSA의 경우, 원래 곡선 상의 한 점에 어떤 수를 곱해 곡선 상의 다른 한 점으로 대응시킨다. 이때 점의 위치 (x_1, y_1)과 (x_2, y_2)를 알고 있더라도 어떤 숫자가 곱해졌는지 알아내기는 무척 어렵다. ECDSA가 RSA보다 파훼하기 더 어렵기 때문에 더 보안성이 높다고 평가된다. 같은 수준의 복잡도를 가진 RSA와 ECDSA를 비교하더라도 커다란 소수를 Key로 사용하지 않아도 되므로 ECDSA의 Key 크기가 더 작다.

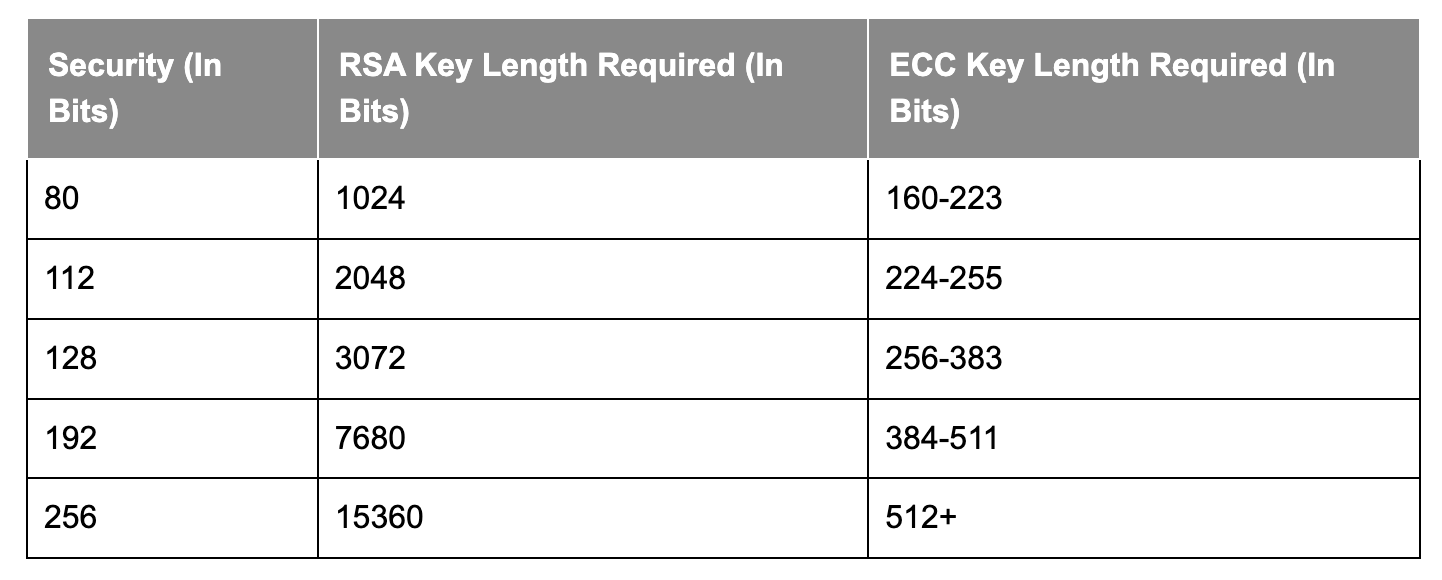
이렇게 하나하나 모든 경우의 수를 시도해보며 암호를 해제하는 공격 기법을 무차별 대입 공격(Brute-force Attack)이라고 하는데, ECDSA는 이런 유형의 공격에 대해 RSA보다 더 견고하다. 뿐만 아니라 ECDSA는 암호 생성에 필요한 네트워크 사용량과 계산량이 RSA에 비해 더 적다. 따라서 웹사이트 등에 암호화 연결을 할 때, ECDSA 기법을 사용하면 더 빨리 웹 사이트를 로딩할 수 있다.

아직까지 모든 인증 기관(Certificate Authority; CA)가 제어 패널이나 하드웨어 모듈에서 ECC를 지원하지는 않지만, 점점 늘어나는 추세이다.

3. 양자 컴퓨터의 위협이 다가온다.

이번 기사에서는 무차별 대입 공격(Brute-force attack)의 측면에서만 암호화 기법을 비교했다. 하지만 암호화 방식을 파훼하는 방법은 이것만 있는 게 아니다. RSA와 ECDSA의 경우, 이론적으로 쇼어 알고리즘(Shor’s Algorithm)으로 풀 수 있다. 연산량이 많은 문제는 특히 양자 컴퓨터가 개발되면 해결된다. 양자비트(Q-bit)를 기반으로 하는 양자 컴퓨터는 동시에 여러 조합을 시도할 수 있고, 현재 슈퍼 컴퓨터보다 30조 배 가까이 연산 속도가 빨라질 것이다. 미국 국립표준기술연구소(NIST)는 양자 컴퓨터가 상용화되면 ECDSA와 RSA를 포함한 공개키 암호화 방식(Public Key Cryptography) 이 실패할 것이라고 예측한다. 오늘날 많은 연구자들이 양자 내성(Quantum immunity)을 갖는 암호화 방식을 개발하기 위해 각지에서 연구중이다.

4. 갈무리

몇 가지 단점에도 불구하고 RSA와 ECDSA는 현재 가장 인기 있는 비대칭 암호화 알고리즘들이다. 해킹 공격에 쉽게 무너지지 않는 튼튼한 보안을 제공하며, 그 기저에는 둘이 서로 다른 원리를 기반으로 한다. 그리고 둘 중 어느 방법을 이용하더라도 최적의 보안을 활용하기 위해서는 제대로 알고리즘을 구현하는 것이 중요하다.

주석

원글 : https://sectigostore.com/blog/ecdsa-vs-rsa-everything-you-need-to-know/

암호기술에 대해 : https://seed.kisa.or.kr/kisa/intro/EgovDefinition.do

전자 서명 및 디지털 서명 : https://terms.tta.or.kr/dictionary/dictionaryView.do?subject=전자+서명