※ 매주 월요일은 무료로 기존처럼 Mathletter가 공유 됩니다. 화요일부터는 멤버십신청을 하신 분들께만 제공됩니다. 스레드에 말씀드렸습니다. 혹시 스레드에서 못보신 분들이 계실까봐 여기에 공유 합니다.
아울러 인원 추가와 시스템 비용과 같은 메스레터 운영으로 인하여 유료로 전환하게 된 점 안내 드립니다.
질문이나 의견 있으신 분들은 메일이나 댓글 부탁드립니다. 감사합니다. 즐거운 한 주 되세요Mathletter 멤버십 변경안내
1. 실수 a, b에 대하여 다음이 성립할 조건을 구하고, 그 이유를 설명하시오.
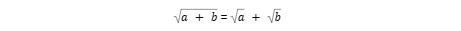

3. n이 자연수일 때, (x − 1)( x − 2)( x − 3)...(x − n) + 1을 전개하면 다항식으로 나타낼 수 있다. 이 다항식에서

4. 두 다항식 P(x) = ax³ + bx² + cx + d와 Q(x) = x² - 3x + 5에 대하여, P(x) ÷ (x - 2) = Q(x)가 항등식으로 성립할 때, 상수 a, b, c, d의 값을 구하시오.
5. 모든 실수 a에 대하여 이차방정식 (a-3)x² + 2ax + (a+3) = 0이 항상 실근을 가질 조건을 구하시오.
6. 이등변삼각형 ABC에서 AB=AC=10이고 ∠BAC=60°이다. 변 BC위의 점 P에 대하여 AB² = AP² + BP² 일 때, 점 P는 변 BC를 어떤 비율로 내분하는지 구하시오.
7. 좌표평면에서 이차함수 y = ax²+bx+ c의 그래프와 직선 y = kx+m이 접할 조건을 a, b, c, k, m으로 나타내시오.




의견을 남겨주세요