목적지 방향이 같은 두 사람이 택시를 함께 타서 돈을 아끼기로 했습니다. A의 목적지까지는 10만 원이 들고, B의 목적지까지는 20만 원이 듭니다. B가 가는 길 중간에 A의 목적지가 있기 때문에 둘이 같이 타도 총 비용은 20만 원이 듭니다. 이렇게 합승한 경우, 총 요금을 두 사람이 어떻게 나누면 공정할까요?
직관적인 방법의 함정
먼저 B가 이렇게 제안합니다. A와 B가 혼자 탔을 때 각각 10만 원, 20만 원이 드니까 A는 1/3, B가 2/3를 부담하자고. 그러면 A는 20만 원x(1/(1+2))=6.7만 원, B는 20만 원x(2/(1+2))=13.3만 원이 됩니다.
금액도 합리적이고 방법도 그럴 듯하다고 생각했지만 그럼에도 A는 뭔가 찜찜함을 느낍니다. 이럴 때 쓸 만한 방법으로, 값을 극단화해 보기가 있습니다.
만약에 B의 원래 택시비가 20만 원이 아니라 1000만 원이면 어떻게 될까요? A의 부담금은 6.7만 원에서 9.9만 원(=1000만 원x(10/(10+1000))으로 올라가고, B는 990.1만 원이 됩니다. A는 달라진 게 하나도 없는데, B의 변화 때문에 A의 부담금이 늘어났습니다. 게다가, 합승 덕분에 절약한 혜택도 거의 B에게만 돌아갔습니다. 뭔가 이상하죠.
섀플리 가치
또 다른 분배 방식으로 섀플리 가치(Shapley Value)를 적용할 수 있습니다. 이는 협력 게임에서 각 참여자가 기여한 정도에 따라 이익을 공정하게 나누는 방법입니다. 위의 택시 합승 문제에 적용하려면, 먼저 경우의 수를 세야 합니다. 이 게임에 A가 참여하게 되는 경우는 2가지입니다.
- {} -> {A}: 아무도 타지 않는 상황에서 A가 타는 경우죠. 이때는 A의 참여로 절약되는 돈은 없습니다. 따라서 기여액은 0.
- {B} -> {A, B}: B 혼자 타는 상황에서 A가 추가로 타는 경우로서, 이때는 (둘이 따로 타면 총 30만 원이 드는데 합승해서) 10만 원을 절약했으므로 기여액은 10만 원.
두 경우의 기댓값(평균)을 구하면 5만 원이 됩니다. B의 경우도 같은 기준으로 계산하면 기여액은 5만 원입니다. 협력으로 얻은 이익을 각자의 기여액 대로 나눠주면 A는 5만 원, B는 15만 원을 부담한다는 결론이 나옵니다.
또 이렇게 생각해 볼 수도 있습니다. A의 목적지까지는 A와 B가 같이 타고 가니까 10만 원을 둘이 절반씩 부담합니다. A가 내린 후부터 발생하는 비용은 B 혼자서 부담합니다. 그래서 A는 5만 원, B는 15만 원. 합리적인가요?
수식이 등장할 시간
위의 경우는 참여자가 2명뿐이라서 쉽게 답을 구했지만, 만약 참여자가 3명 이상으로 늘어나면 직관만으로는 계산이 어렵습니다. 수식의 도움이 필요합니다.
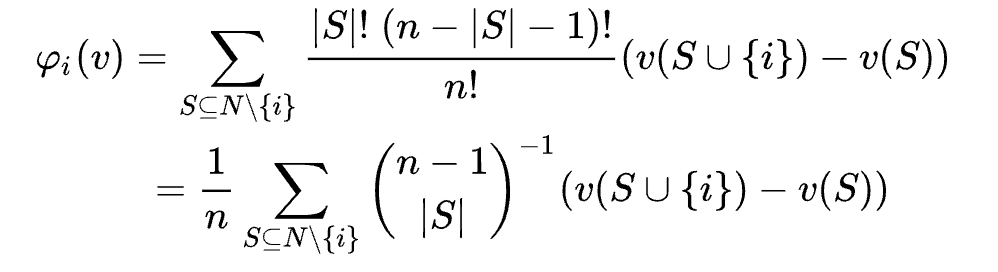
플레이어 i가 협력에 참여하게 되는 각 경우들에서, i의 참여 덕분에 발생한 추가 이익(한계 기여도)의 가중평균을 구하게 됩니다. 참여자가 3명인 경우에 적용해 보면,
- A가 혼자 참여하는 경우의 기여도
- A가 다른 1명과 협력하는 경우들의 평균 기여도
- A가 다른 2명과 협력하는 경우의 기여도
의 평균입니다. 기호 때문에 좀 헷갈릴 수 있지만 의도와 의미 모두 매우 직관적입니다.
협력해야 하는데, 서로 본심을 숨긴다면?
그런데... 이런 배분이 공정해 보인다고 하더라도, 강제할 방법은 없습니다. 누구 한 명이라도 동의하지 않으면 협상은 결렬됩니다. 위의 경우에는 그나마 각자의 원래 요금을 알고 있었기 때문에 수월하게 풀렸지만, 플레이어들이 서로 협력하지 않는다면, 가령 원래 비용을 속이거나 협력에 대한 선호를 감추는 상황에서는 공정한 분배 방법을 찾기가 까다롭습니다.
다음 글에서는 그런 문제에 대한 해결책을 논의해 보겠습니다. (과장광고 방지 차원에서 미리 얘기하면, 완벽한 해결책은 없습니다. 그래도 고려해 볼 만한 아이디어는 있습니다.)
참고 자료
- 하임 샤피라, 『n분의 1의 함정』, 이재경 옮김, 반니(2017)





의견을 남겨주세요