양자 컴퓨터 10분 총 정리

Comment.

Fig.1 양자도 계산할 수 있다 - 폴 베니오프

1961년, 롤프 란다우어Rolf Landauer 는 정보가 소실되는 비가역적 연산이 필연적으로 에너지(열) 소모를 동반한다는 사실을 밝혔습니다. 이 원리는 ‘정보’가 곧 물리적 현실로 이어진다는 것을 의미합니다. 그렇다면 반대로 정보를 지우지 않고 입력을 항상 복구할 수 있는 연산(가역적 컴퓨터)을 실현하면, 이론적으로 에너지 소모 없는 계산도 가능하다는 이야기가 되죠.

1980년, 폴 베니오프Paul Benioff 는 이러한 아이디어를 양자물리학과 접목시켜, 정보의 손실없이 에너지를 낭비하지 않는 컴퓨터 모델을 논문 <물리적 시스템으로서의 컴퓨터: 튜링 머신으로 표현된 컴퓨터의 미시적 양자역학적 해밀턴 모델>에서 발표합니다. 해밀토니언은 입자 또는 시스템이 가진 총 에너지를 나타내며, 이 값과 슈뢰딩거 방정식을 이용하면 시간에 따른 양자상태의 변화를 예측할 수 있습니다. 베니오프는 이를 이용해 컴퓨터의 계산 모델인 튜링 머신이 양자역학적 해밀토니언 연산자로 표현될 수 있음을 보였습니다. 컴퓨터도 양자 물리 법칙에 따라 작동할 수 있다는 가능성을 제시한 것이죠.

Fig.2 그래서 양자컴퓨터가 필요하다 - 리처드 파인만

리처드 파인만Richard Feynman 은 폴 베니오프의 양자계산 모델에서 한 걸음 더 나아가, 양자컴퓨터가 반드시 필요한 실질적 이유를 제시했습니다.

파인만은 입자가 한 지점에서 다른 지점으로 이동할 때 하나의 경로만이 아니라 가능한 모든 경로를 동시에 지나간다는 ‘경로적분’ 해석으로 양자 세계를 설명했습니다. 이때 각 경로에 ‘확률 진폭’이라는 양자적 값을 더합니다. 여러 경로의 진폭을 더하고 그 크기를 제곱하면, 입자가 실제로 그곳에 있을 확률이 계산됩니다.

하지만 이런 양자 현상을 고전 컴퓨터로 시뮬레이션하려 하면 상태의 수가 2ⁿ씩 폭발적으로 늘어나 계산이 불가능해집니다. 파인만은 이를 단순한 기술 문제가 아니라 고전 컴퓨터 자체의 한계로 보았습니다. 자연이 양자역학적이라면, 자연을 흉내 내는 컴퓨터도 양자역학적이어야 한다는 결론에 도달한 것이죠.

1982년에 발표한 <컴퓨터를 이용한 물리 현상 시뮬레이션> 논문에서 그는 연속시간 양자 워크라는 개념도 제시합니다. 고전적 랜덤 워크가 ‘한 칸씩 무작위로 이동’하는 것이라면, 양자 워크에서는 입자가 모든 방향으로 동시에 퍼져 나가며 이동합니다. 양자 중첩 현상이 일어나는 것이죠. 계산도 ‘1초마다 한 칸’처럼 단계별 명령이 아닌, 해밀토니언에 의해 끊김 없이 자연스럽게 흐르는 과정이 됩니다.

이로써 파인만은 실제 물리 세계의 법칙을 그대로 따르는 ‘양자컴퓨터’가 반드시 필요하다는 학문적·기술적 근거를 제시했으며, 이는 이후 모든 양자컴퓨터 연구와 구현의 출발점이 되었습니다.

Fig.3 양자 컴퓨터의 계산법 - 데이비드 도이치

파인만이 “왜 양자 컴퓨터가 필요한가”를 제시했다면, 1985년, 데이비드 도이치David Deutsch 는 “어떻게 양자 컴퓨터가 가능한가”를 증명했습니다.

당시에는 ‘세상에서 가능한 모든 계산은 튜링 머신으로 표현할 수 있다’는 처치–튜링 명제Church–Turing Thesis 가 널리 받아들여지고 있었습니다. 하지만 도이치는 이 명제가 고전 물리학의 세계에만 해당된다고 보았습니다. 그는 자연이 실제로는 양자 법칙에 따라 움직이므로, 계산의 이론 또한 양자역학적 체계로 새롭게 정의해야 한다고 주장했습니다.

그가 제안한 ‘도이치–요샤 알고리즘Deutsch–Jozsa Algorithm’은 양자역학적으로 작동하는 컴퓨터를 보여줍니다. 쉽게 예를 들어, 누르면 항상 불이 켜지는 버튼이 있고, 1/2 확률로 켜지는 버튼이 있다고 해봅시다. 이때 일반 컴퓨터가 어떤 종류의 버튼인지 알기 위해서는 모든 버튼을 하나씩 눌러봐야 합니다. 반면 양자컴퓨터는 중첩 상태를 이용해 모든 버튼을 한 번에 눌러보는 것과 같은 계산을 할 수 있습니다. 그리고 계산이 끝나면 간섭 현상이 일어나 정답에 해당하는 정보는 서로 더해져 강해지고, 불필요한 정보는 서로 지워져 사라집니다.

도이치는 이처럼 중첩과 간섭을 이용한 병렬 탐색과 정보 증폭이라는 양자계산의 핵심 원리를 처음으로 증명함으로서 양자컴퓨터 시대의 문을 열게 되죠.

Fig.4 양자 컴퓨터가 진짜 실용적인 이유

파인만이 “왜 양자 컴퓨터가 필요한가”를 제시하고, 데이비드 도이치가 “어떻게 양자 컴퓨터가 가능한가”를 증명했다면, 피터 쇼어Peter Shor 와 로브 그로버Lov Grover 는 “양자 컴퓨터가 얼마나 실효성이 있는가”를 보여주었습니다.

① 피터 쇼어

피터 쇼어는 1994년 고전 컴퓨터로는 사실상 해결할 수 없던 큰 수의 소인수분해 문제를 양자 알고리즘으로 빠르게 계산할 수 있음을 보여주었죠. 소인수분해 문제는 우리가 매일 쓰는 RSA 공개키 암호체계의 핵심입니다. 예를 들어, A가 323이라는 수를 공개키로 내놓고 “누구나 이걸로 암호를 걸어 보내라”고 말한다고 해보죠. B는 이 숫자를 이용해 메시지를 암호화해 보냅니다. 하지만 암호를 다시 풀 수 있는 사람은 323을 정확히 나눌 수 있는 비밀 숫자, 즉 ‘개인키’를 가진 A뿐입니다. 다른 사람은 323이 어떤 두 수의 곱인지(예를 들어 17×19)를 알아내지 못하면 암호를 풀 수 없죠.

소인수분해 문제를 푸는 방법은 다음과 같습니다. 예를 들어 N=15를 소인수분해하고 싶다면, 먼저 15와 서로소인 숫자를 고릅니다. 여기서는 a=2라고 해보겠습니다. 이제 2^n/15의 나머지 값을 출력해보면 2→4→8→1이 반복됩니다. 즉, 주기 r=4입니다. 주기 r이 짝수일 때, (a^(r/2) ± 1)과 N의 최대공약수를 구하면 N의 소인수를 구할 수 있습니다. 여기서는 (2^(4/2)± 1)과 15의 최대공약수를 구하면 15=3×5라는 소인수가 나옵니다.

고전 컴퓨터는 이런 주기를 찾으려면 x=1부터 차례로 계산해야해서 엄청난 시간이 걸립니다. 수백 자리의 수를 분해하는 데 수천 년이 걸릴 수도 있죠. 하지만 양자 컴퓨터는 모든 x값을 동시에 중첩시켜 한 번에 계산을 마칩니다. 그리고 양자 푸리에 변환(QFT)을 이용해 계산 결과 속에 숨어 있는 “주기 r”을 추출해냅니다. 하지만 만약 주기가 홀수라면 r/2이 정수가 되지 않기 때문에 (a^(r/2) ± 1)이라는 식을 쓸 수 없습니다. 이때는 실패 처리하고 다른 a값을 선택해 다시 시도합니다. 이 실패 값들은 간섭으로 서로 지워지고, 정답에 해당하는 주기만 남습니다.

양자컴퓨터는 이 과정을 빠르게 반복할 수 있기 때문에 몇 번만 반복해도 높은 확률로 짝수 주기를 찾아낼 수 있습니다. 이렇게 해서 고전적으로는 사실상 불가능했던 소인수분해를 짧은 시간 안에 해결할 수 있게 된 거죠.

② 로브 그로버

로브 그로버는 1996년, 무작위로 정렬되지 않은 데이터 속에서 원하는 정보를 훨씬 빠르게 찾아내는 ‘그로버 알고리즘’을 제시합니다. 이 알고리즘은 ‘정답의 확률’을 점점 키워가는 독특한 방식을 보여주었습니다.

핵심 아이디어는 ‘모든 데이터를 동시에 살펴보는 중첩’ 상태에서 출발합니다. 양자컴퓨터는 처음에 모든 데이터가 동시에 존재하는 중첩 상태를 만듭니다. 그리고 그중 정답에 해당하는 상태에만 특별한 표시를 해주죠. 이 과정을 오라클Oracle 이라고 부르는데, 정답 상태에만 ‘-1’을 곱해 위상이 반전되도록 만듭니다.

그다음엔 ‘평균에 대한 반전’이라는 과정을 수행합니다. 이건 전체 상태들의 평균을 기준으로 각 신호의 세기를 뒤집는 과정입니다. 이 과정을 거치면, 정답으로 표시된 상태의 신호가 조금 더 강해집니다.

이 두 단계를 반복하면, 정답 상태의 진폭은 점점 커지고 나머지 오답 상태들은 점점 작아집니다. 그래서 마지막에 측정했을 때, 정답이 선택될 확률이 압도적으로 높아지는 것이죠. 이를 통해 1만 개의 데이터 중 하나를 찾는 데 고전 컴퓨터가 평균 5천 번의 시도가 필요한 반면, 그로버 알고리즘은 약 100번 정도만으로 원하는 답을 찾을 수 있습니다.

Fig.5 양자역학, 전자회로에서 구현 가능할지도?!

이론적 토대가 만들어지고 있는 가운데 실험적 토대도 함께 만들어지고 있었습니다. 1980년대 중반, 존 클라크John Clarke 는 조셉슨 접합(두 개의 초전도체 사이에 매우 얇은 절연층을 끼워 넣은 구조)을 이용한 전기 회로에서 전자가 양자역학적으로 움직이는 것을 발견합니다. 양자역학이 실제 전자 회로에서도 작동한다는 사실을 증명한 것이었죠. 이 발견은 전기를 이용해 정보를 저장하고 조작하는 양자컴퓨터의 핵심 부품인 큐비트qubit* 를 만드는 데 기초가 되었습니다.

미셸 드보레Michel Devoret 와 존 마티니스John Martinis 는 클라크의 연구를 계승하여 초전도 회로 안에서 양자 상태를 더 안정적이고 정밀하게 다루는 기술을 개발했습니다. 드보레는 초전도 회로 내에서 양자 상태를 안정적으로 유지하고 측정하는 기술을 발전시켰고, 마티니스는 이를 기반으로 실제 초전도 큐비트를 집적·조작하는 시스템을 구축했습니다. 이들의 연구는 훗날 IBM, 구글, 인텔 등이 사용하는 초전도 양자컴퓨터 아키텍처의 직접적인 시초가 되었습니다.

*큐비트란?

일반 컴퓨터는 정보를 0 또는 1의 형태로 저장합니다. 하지만 큐비트는 양자역학의 원리를 이용해 0과 1이 동시에 존재할 수 있는 상태를 가질 수 있습니다. 이 현상을 ‘중첩’이라고 부릅니다. 또한 두 개의 큐비트가 서로 얽혀 있으면, 한쪽의 상태가 바뀔 때 다른 쪽도 즉시 영향을 받습니다. 이런 특성 덕분에 양자컴퓨터는 기존 컴퓨터보다 훨씬 빠르고 복잡한 계산을 동시에 수행할 수 있습니다.

Fig.6 양자 컴퓨터 진짜 만들어 봄 - 아이작 추앙

1997년, 아이작 추앙Isaac Chuang 은 IBM 연구소에서 세계 최초로 2비트 양자컴퓨터를 개발했습니다. 드디어 양자컴퓨터가 실제 물리적으로 구현될 수 있음을 증명한 것이었죠.

아이작 추앙은 NMR(핵자기공명)이라는 기술을 활용했습니다. 이 기술은 원자핵을 강한 자기장에 두고, 라디오파를 쏘아 그 상태를 정교하게 조종하는 방식입니다. 추앙은 이 원자핵의 상태를 '큐비트'로 사용했죠. 이 과정에서는 중첩을 만들어주는 연산인 하다마드Hadamard 와 두 큐비트를 얽히게 해주는 연산인 CNOT(Controlled-NOT) 같은 대표적인 양자 게이트가 쓰였습니다. 추앙은 이런 양자 게이트 동작을 라디오파 펄스로 실제로 구현한 것이었죠.

하지만 핵자기공명(NMR) 기술은 다수의 큐비트를 효과적으로 확장하는 데 한계가 있었고, 큐비트 간의 상호작용을 정밀하게 제어하는 데 어려움이 있었습니다. 게다가 NMR 기반 큐비트는 중첩과 얽힘 상태를 유지하는 시간이 짧아 양자 상태의 안정성을 오래 유지하기 어렵고, 이로 인해 오류가 발생하기 쉽다는 문제가 있었습니다. 양자 게이트 연산을 수행하는 라디오파 펄스도 정밀도가 완벽하지 않아 누적된 오차가 계산 결과에 영향을 미칠 수 있었습니다. 이러한 한계들 때문에 아직 제대로 활용되기에는 역부족이었죠.

Fig.7 양자 컴퓨터 판매 시작합니다

NMR 양자컴퓨터의 예에서 보다시피, 큐비트는 0과 1이 동시에 존재하는 중첩 상태를 만들 수 있어야 합니다. 하지만 이 중첩 상태는 아주 작은 노이즈나 외부 자극에도 쉽게 깨지기 때문에, 양자 게이트 방식으로는 많은 수의 큐비트를 안정적으로 제어하기가 매우 어려웠습니다.

그런 와중에 2007년 D-웨이브 시스템즈D-Wave Systems 에서 세계 최초로 양자컴퓨터 시제품을 발표했습니다. 이는 D-웨이브가 기존의 양자 게이트 방식이 아닌, ‘양자 어닐링’ 방식을 채택했기 때문에 가능한 일이었죠.

컴퓨터는 0과 1의 이진법을 사용하는 디지털 컴퓨터와 연속적인 값을 사용하는 아날로그 컴퓨터가 있습니다. 아날로그 컴퓨터에서는 계산을 위해 어닐링이라는 방법을 많이 사용합니다. 어닐링이란 금속의 온도를 높였다가 서서히 식히는 과정에서 원자들이 가장 안정된 상태, 즉 에너지가 가장 낮은 자리로 배열되는 현상을 말합니다. 이때 원자들이 천천히 움직이며 규칙적으로 정렬되면 결함이 줄어들고 금속은 더 단단해집니다.

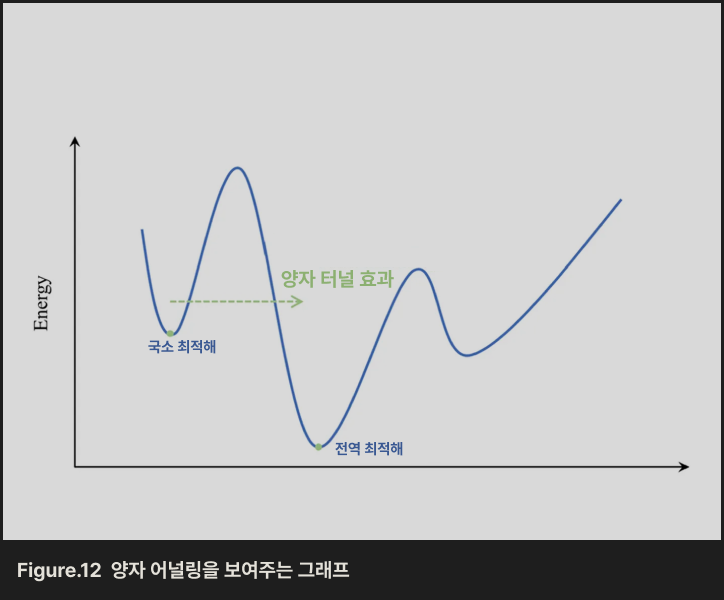
이 원리를 계산에 응용한 것이 어닐링 계산입니다. 만약 어떤 수학적 문제나 함수가 알갱이의 위치에너지 함수와 같은 구조를 가진다면, 그 함수의 최솟값은 곧 가장 낮은 에너지 상태, 즉 가장 좋은 해답과 같습니다. 따라서 시스템의 ‘온도’를 천천히 낮추면서 자연이 스스로 에너지를 최소화하도록 기다리면 결국 우리가 찾는 답에 도달하게 되는 것이죠.

양자 어닐링은 이 과정을 양자역학적으로 확장한 계산 방식입니다. 큐비트에 직접 연산을 가하지 않고, 큐비트의 온도를 낮추거나 자기장을 걸어준 뒤 그들이 스스로 가장 낮은 에너지 상태로 이동하도록 기다립니다. 그리고 최종적으로 도달한 상태를 관측해 답을 얻습니다. 이 점만 놓고 보면 고전 어닐링과 크게 다르지 않는데요. 양자 어널링의 결정적 차이가 하나 있는데, 바로 양자 터널 효과입니다.

고전적인 어닐링에서는 입자가 높은 장벽에 막히면 그 너머의 더 낮은 에너지 상태로 이동하지 못합니다. 하지만 양자 어닐링에서는 입자가 마치 산을 통과하듯, 터널을 뚫고 더 낮은 에너지 상태로 이동할 수 있습니다. 이 덕분에 시스템은 훨씬 빠르게, 그리고 더 효율적으로 전역 최적해(global minimum)에 도달할 수 있습니다.

이 방식 덕분에 D-웨이브는 범용 계산은 어렵지만, 물류, 교통, 금융, 화학 등에서 자주 등장하는 복잡한 최적화 문제를 실제 산업 수준에서 풀 수 있는 실용적 양자컴퓨터를 내놓을 수 있었습니다.

Fig.8 현재는 양자컴퓨터 춘추전국시대

D-웨이브의 등장을 계기로 IBM, 구글, 인텔, 마이크로소프트 등 전 세계 주요 기업들이 본격적으로 양자컴퓨터 경쟁에 뛰어들었습니다. 각 회사는 초전도, 이온덫, 중성원자, 광, 양자점, 점결합, 위상 등 서로 다른 접근 방식을 취했는데요. 주요 접근 방식은 다음과 같습니다.

① 초전도 양자컴퓨터 - IBM, 구글, D-웨이브

초전도 양자컴퓨터는 전기 저항이 0인 ‘초전도체’를 이용해 만든 양자컴퓨터입니다. 보통 전선에는 저항이 있어서 전류가 금방 사라지지만, 초전도체로 고리를 만들면 전류가 한 번 흐르기 시작하면 멈추지 않고 계속 돌죠. 이 특성을 이용해 전류가 시계 방향으로 흐를 때를 0, 반시계 방향으로 흐를 때를 1로 정해 큐비트로 사용합니다. 전류의 방향이 두 가지 상태를 동시에 가질 수도 있는데, 그게 바로 양자 중첩 상태입니다. 이 고리들은 미세한 자석처럼 자기장을 만들어내고, 서로 가까이 두면 밀거나 당기며 상호작용을 합니다. 이를 이용해 두 큐비트를 연결하고 계산을 수행하는 것이죠.

이 양자컴퓨터의 CPU는 고전적인 컴퓨터 칩처럼, 기판 위에 초전도 물질로 고리를 그려서 만듭니다. 여기에 마이크로파를 보내 정보를 읽고 쓰며 큐비트를 조작하죠. 다만 큐비트의 수를 늘리는 일은 쉽지 않습니다. 하나의 큐비트마다 여러 개의 전선이 연결되어 있어서, 수백 개만 돼도 냉동기 안이 전선으로 가득 차 복잡해지죠. 또한 큐비트가 많아지면 계산 시간이 길어지고, 큐비트가 중첩과 얽힘 상태를 유지할 수 있는 ‘결맞음 시간’보다 길어지면 계산이 흐트러져 버립니다. 그래서 많은 큐비트를 안정적으로 제어하고 유지하는 것이 초전도 양자컴퓨터의 가장 큰 과제입니다.

② 이온덫 양자컴퓨터 - IonQ, Quantinuum

이온덫 양자컴퓨터는 ‘이온’을 전기장으로 잡아두고 레이저로 조작해 큐비트로 사용하는 방식입니다. 이온은 전기적으로 조작하기 쉬워, 정해진 공간 안에 떠 있는 채로 두 가지 에너지 상태를 0과 1로 사용할 수 있죠. 전자기파를 쏘면 이온의 상태가 바뀌거나 두 상태가 동시에 존재하는 중첩 상태가 만들어집니다. 여러 이온은 함께 진동하며, 이 진동을 이용해 큐비트끼리 상호작용하게 합니다.

하지만 한 덫에 너무 많은 이온을 잡아두면 서로 영향을 주어 오류가 생기기 때문에, 보통 100개 정도가 한계죠. 이를 해결하기 위해 여러 개의 CPU를 광섬유로 연결하거나, 이온을 잠시 다른 CPU로 옮겨 연산하는 방법이 연구되고 있습니다.

③ 중성원자 양자컴퓨터 - QuEra, Pasqal

이온덫 양자컴퓨터와 비슷하지만, 이온 대신 전하가 없는 중성원자를 이용하는 방식입니다. 강한 레이저로 원자를 한 점에 붙잡아 두는 광집게 기술이 등장하면서 가능해졌죠. 이렇게 잡은 원자의 두 가지 에너지 상태를 0과 1로 정해 계산을 하며, 단일 큐비트 연산은 전자기파로 수행합니다.

또한 레이저로 광집게의 위치를 옮기면 원자도 함께 움직이기 때문에, 두 원자를 가까이 붙여 상호작용하게 하고 다시 제자리로 돌려놓을 수 있습니다. 이런 방식으로 이중 큐비트 연산을 수행하죠. 2023년에는 49개의 원자를 격자 모양으로 배열하고 서로 포개어 연산을 수행한 실험이 발표되기도 했습니다.

④ 광 양자컴퓨터 - Xanadu, PsiQuantum

광 양자컴퓨터는 빛의 알갱이인 광자의 성질을 이용한 양자컴퓨터입니다. 편광 방향에 따라 수직이면 0, 수평이면 1로 정하고, ‘파장판’이라는 장치를 이용해 편광 방향을 바꾸면서 큐비트 상태를 조작합니다. 이 기술의 가장 큰 장점은 빛의 속도로 연산이 이루어진다는 점입니다. 광자는 질량이 없고 환경과 거의 상호작용하지 않기 때문에 결맞음 시간이 매우 길죠. 즉, 양자 정보가 쉽게 깨지지 않습니다.

하지만 광자는 흡수되거나 사라질 수도 있다는 단점이 있습니다. 또 자연상태에서는 서로 상호작용하지 않기 때문에 얽힘(이중 큐비트 연산)을 만들기가 어렵고, 확률적으로만 가능합니다. 큐비트 수가 많아질수록 이러한 확률적 얽힘 과정이 누적되어 계산의 정확도가 급격히 떨어지는 문제가 있습니다. 또한 광 양자컴퓨터는 계산을 수행하는 광학소자들이 공간에 고정되어 있어, 알고리즘을 바꾸려면 장치의 배열 자체를 바꿔야 했습니다. 그래서 크기가 커지고 실용성이 떨어졌죠.

최근에는 이런 소자를 광학 집적회로 형태로 만들어 소자의 배영을 바꾸는 대신 프로그램으로 조작할 수 있도록 만드는 연구가 진행 중에 있습니다.

⑤ 양자점 양자컴퓨터 - Intel, Quantum Motion

양자점은 전자를 가두어 둘 수 있는 나노 크기의 공간으로, 마치 인공적인 원자처럼 작동합니다. 여기에 자기장을 걸면 전자의 스핀이 ‘위쪽(Up)’과 ‘아래쪽(Down)’ 두 상태로 나뉘고, 이를 각각 0과 1로 사용합니다. 전자기파를 쏘면 두 상태가 전환되면서 단일 큐비트 연산이 이루어지고, 두 양자점 사이의 상호작용을 조절해 이중 큐비트 연산을 수행합니다.

이 방식의 장점은 자연에 존재하는 분자를 그대로 큐비트로 사용하는 방식과 달리 우리가 원하는 구조의 큐비트를 만들 수 있다는 점입니다. 하지만 인공적으로 만든 양자점은 외부와 상호작용이 많고, 큐비트 간의 제어가 어렵다는 단점이 있습니다.

⑥ 점결합 양자컴퓨터 - Quantum Brilliance, Quantum Diamonds

점결합 양자컴퓨터는 결정(크리스탈) 안의 불순물이나 결함을 이용해 큐비트를 만드는 방식입니다. 예를 들어, 실리콘 결정 속에 인(P) 원자를 하나 넣으면 전자가 하나 더 생기면서 마치 공중에 떠 있는 단일 원자처럼 동작하죠. 이런 환경은 외부 간섭이 적어 큐비트로 사용하기 좋습니다.

또 다른 예로, 다이아몬드의 NV 센터가 있습니다. 이는 탄소 대신 질소가 들어가고 인접한 탄소 하나가 빠져나간 결함 구조로, 외부 간섭을 거의 받지 않으며 결맞음 시간이 매우 깁니다. NV 센터의 두 스핀 상태를 0과 1로 사용하고, 여기에 마이크로파나 광파를 쏘아 연산을 수행합니다. 하지만 NV 센터를 원하는 위치에 정확히 만들어내기 어렵다는 단점이 있습니다.

⑦ 위상 양자컴퓨터 - Microsoft, Quantinuum

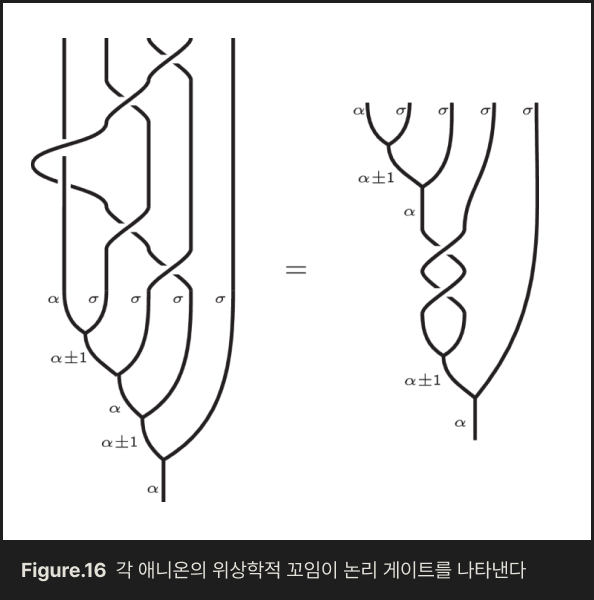
위상 양자컴퓨터는 완전히 다른 접근을 합니다. 이 방식은 정보를 입자 하나의 상태에 저장하지 않고, 여러 입자들의 상대적인 배치(꼬임) 에 저장합니다. 여기에는 ‘애니온Anyons’이라는 특수한 입자들이 등장하죠. 애니온들이 서로를 감싸며 움직인 궤적이 머리카락을 땋은 모양처럼 꼬이는데, 바로 이 꼬임의 형태가 정보가 됩니다.

이 방식의 강점은 잡음과 오류에 강하다는 점입니다. 개별 입자의 위치는 환경에 의해 흔들릴 수 있어도, 여러 입자가 만든 전체적인 꼬임 구조는 쉽게 변하지 않기 때문이죠. 그래서 이론적으로는 거의 완벽한, 즉 ‘무오류’에 가까운 계산이 가능하다고 여겨집니다. 다만 아직 애니온이 실제로 존재한다는 확실한 실험적 증거는 발견되지 않았습니다.

이번 뉴스레터는 ≪퀀텀의 시대≫와 ≪퀀텀의 세계≫ 두 책의 도움을 많이 받았습니다. 두 책 모두 국내 양자 컴퓨터 연구의 권위자로 꼽히는 이순칠 교수의 저서입니다.

이렇게 생소하고 어려운 분야에 대해서 접근할 때는 쉬운 내용으로 맥락을 먼저 잡고, 디테일한 부분을 좀 더 어려운 책으로 채워넣는데요. 두 책은 그 두 역할을 모두 적절하게 해주는 책이었습니다. 맥락을 잡기에도 어렵지 않았고, 양자 컴퓨터에 대한 다양한 부분을 설명하고 있어 디테일한 부분을 채우기에도 좋은 책이었습니다.

이번 글을 쓰면서 가장 어려웠던 부분은 양자컴퓨터가 가진 수학적 구조를 너무 어렵지 않게, 또 너무 단순하지 않게 풀어내는 일이었습니다. 가능한 한 간략하게 정리하려고 했지만, 설명해야 할 개념이 많다 보니 뉴스레터가 다소 길어졌습니다. 그럼에도 이번 글에서 다 다루지 못한 부분이 여전히 많습니다. 특히 양자컴퓨터의 미래 전망, 어디에 활용될 수 있는지, 그리고 장단점은 무엇인지 같은 내용이 궁금하시다면 ≪퀀텀의 시대≫를 읽어보시길 권합니다. 이 뉴스레터에서 미처 다하지 못한 양자 컴퓨터에 대한 이야기를, 그 책에서 자연스럽게 이어서 보실 수 있을 것입니다.

Reference.

Fig.1

*Since 2021.04
*격주에 한 번 발송하려고 노력합니다.
*<사소한 것들의 역사>, <최초의 브랜드>, <사소하지 않은 것들의 역사>를 조사하고 있습니다.

홈페이지 | https://www.fig1.kr/history

궁금한점이 있다면 | https://forms.gle/ZfXb6UWUkz4HNzAx7

<사소한 것들의 역사>의 내용은 모은 책 <모든 것에 대한 모든 것> | 보러가기↗️

광고성 수신 동의에 동의하지 않으신 경우 뉴스레터 맨 아래 '구독 취소' 링크를 눌러 의사를 표현해주시면 감사드리겠습니다. 구독 해지를 하지 않으신 경우 메일리를 통한 구독 동의와 광고성 수신에 재동의하시는 것으로 진행하고자 합니다.