
한국에서 일간 신규 코로나 바이러스 감염자가 지난 주에 1000명을 넘었어. 예전에는 회사나 학교, 종교시설 등에서 일어나는 집단 감염이 신규 감염자의 많은 부분을 차지했던 반면, 소규모 감염, 즉 일상에서 만나는 개인과 개인, 작은 규모의 모임 등이 전체 감염에서 차지하는 비율이 예전보다 증가했다고 해.
한편 이번 코로나 바이러스의 사태를 통해, 역학 (疫學, Epidemiology) 이라는 학문 분야가 많이 관심을 받기도 했어. 역학은 어떤 인구 집단 안에서 전염병이 어떻게 퍼지고 분포하는지, 어떤 요인이 어떤 영향을 끼치는지 등을 다루는 학문이야. 어떻게 보면, 많은 의학 분야가 이미 벌어진 병과 이에 대한 증상을 다룬다면, 전염병을 예방하기 위한 방법을 공부하고 찾는 의학의 한 분야야. 즉, 전략적으로 어떻게 전염병을 퍼트리지 않을지 고민하는 학문이지.
코로나 바이러스와 관련된 기사들을 많이 접하고, 한편 거리두기로 인해 집에서 방콕하며 알고리즘을 공부하다 과연 역학에서 다룰 수 있는 알고리즘 문제가 뭐가 있을까? 한번 고민해 봤어. 자료를 찾아보니 예전에 수업에서 다룬 적 있는 내용이 나오기도 하고, 지금 하는 일과 직접적으로 관련된 이론이 나오기도 하더라고. 오늘 그래서 이 내용들을 한번 소개해 볼까 해.
그래프 이론 (Graph theory)
그래프 이론은 어떤 개체와 다른 개체의 속성을 설명하기 위해 점과 변 (vertex - edge, node - link) 을 이용하는 이론이야. 특히 이산 수학을 배운다면, 다루게 되는 내용이야. (개인적으로, 수리 가형에서 미적분을 꼭 선택하여 배워야 했던 고딩이었던 입장에서, 고등학생 때 이산 수학 심화 과정을 배우지 않았던 게 좀 아쉬워!) 그래프 이론의 예를 찾아보자면, 버스, 기차, 비행기를 타고 서울에서 대전과 대구를 들러 부산까지 가는 경우의 수를 찾는 문제 등이 있어. 이처럼 도시 - 서울, 대전, 대구, 부산 - 와 같이 이산적으로 딱! 떨어지는 (연속적이지 않으니 점으로 분리하여 볼 수 있겠지?) 문제에서 효율적인 방법이야.
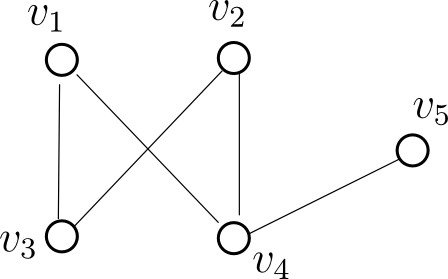
그림과 같은 경우는 간선의 종류가 한 가지 이지만, 이를 양방향이나 단방향으로 정의 할 수도 있어. 아주 간단한 그래프의 경우 주어진 점과 간선의 집합으로 정의할 수도 있어.
네트워크 이론 (Network theory)
위의 그래프 이론을 조금 더 확장시킨 개념이야. 그래프 이론을 조금 더 큰 계 - 예를 들면 용인시에 거주 하는 모든 사람 - 에 적용하여 그 큰 계의 성질을 연구하는 학문이야. 크게 보았을 때, 이 군집이 갖는 어떤 대칭성이나 속의 작은 군집의 영향, 가중치 등을 연구하는 거야. 이러한 성질 때문에, 자연과학 분야 뿐만 아니라 경제학, 사회학 등에서도 많이 쓰여.
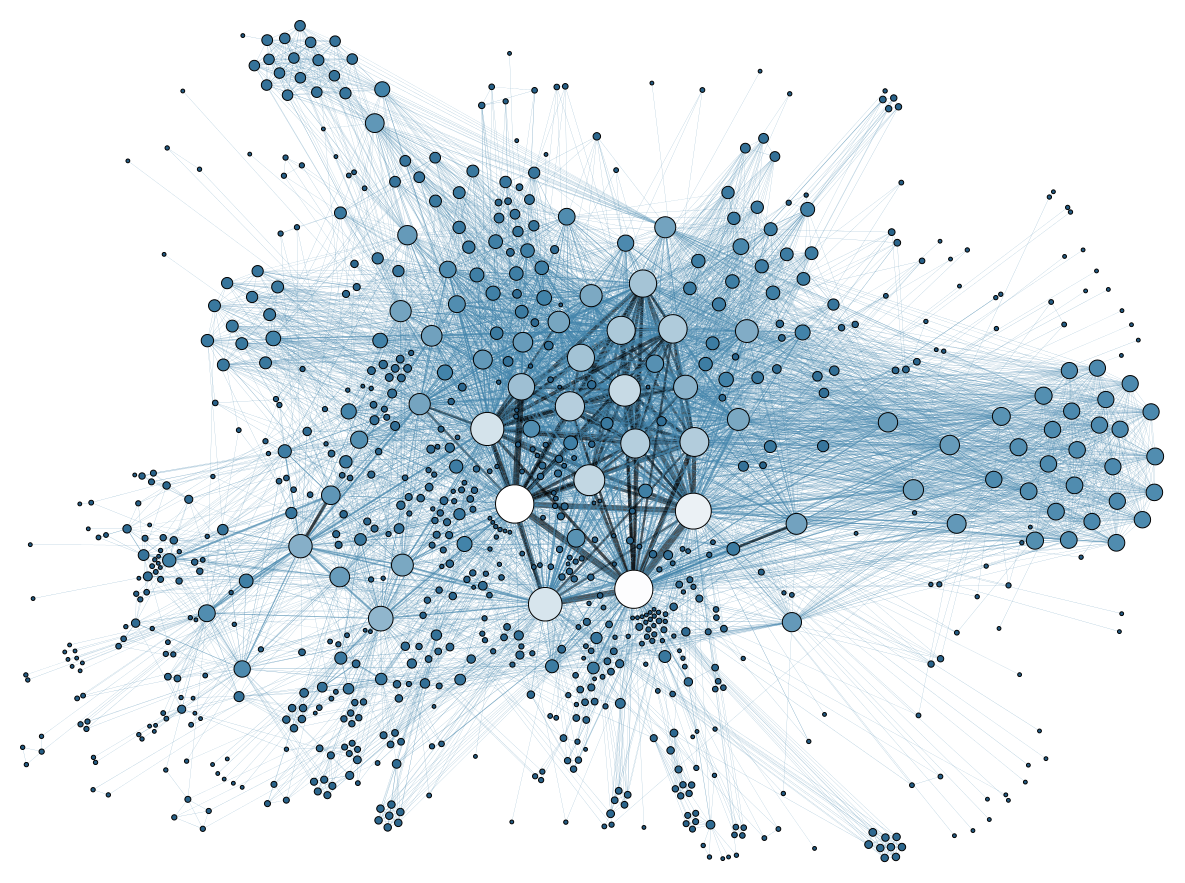
위의 예로만 봐도 단적으로 알 수 있는데, 네트워크 이론은 인간관계를 수치화된 정보로 표현할 수 있는 장점이 있어서, 사회 네트워크를 연구하는 데 많이 쓰이기도 해. 위의 사진의 한 원을 한 사람의 페이스북 계정이라고 하고, 서로 친구인 경우 두 원 사이에 선을 긋는다고 생각해 보면 이해가 더 빠를거야. 이런 관계들 중심에서 인간 관계에서 주요한 역할을 하는 사람들을 바로 한 눈에 알 수 있고, 내가 어떤 사람들과 친목질(?)을 하는지 빠르게 이해할 수 있어.
침투 이론 (Percolation theory)

드디어 침투 이론이다! 침투 이론은 그래프 이론, 네트워크 이론처럼 어떤 큰 계가 점과 선, 즉 연결되어 있는 네트워크의 성질을 갖는다는 점에서 시작하는 포인트는 같아. 침투 이론에서는, 두 노드가 연결되어 있다는 특성을 이용하여, 어떤 전파가 이 선을 이용해 일어난다고 가정하고, 이 전파 과정을 설명하는 이론이야. 따라서, 코로나 바이러스가 퍼지는 경우가 이 침투 이론으로 설명될 수 있고, 산불이 퍼진다거나, 유체의 이동 과정 등의 연구에 쓰이기도 해.
만약 산불이 퍼지거나, 코로나 바이러스가 퍼진다고 하자. 사실 사람들의 주된 관심사는 어떻게 이를 늦추느냐, 아주 많은 시간이 흐른다고 할 때, 얼마나 많은 사람들이 전염병에 걸리느냐? 거든. 침투 이론에서는 이를 중요하게 다루고, 이를 임계 현상으로 설명해.
예를 들면, 경기도에 일정 비율로 코로나 바이러스에 면역을 가진 사람들이 있다고 하자. 시간이 지나도 전염병이 변이를 일으키지 않고, 전염성이 일정한 성질을 갖는다고 하자. 이 때, 그 비율이 특정 임계 값 보다 클 경우, 코로나 바이러스는 시간이 지나도 모든 사람을 전염시킬 수 없어. 하지만, 그 비율이 임계 값 미만일 경우, 사람들은 대부분은 전염된다고 해. 이런 임계 현상이 침투 이론의 아주 중요한 성질이야.
침투 이론의 임계 현상은 이미 수학적으로 증명 되었는데, 이차원 격자 (Nx * Ny) 가 있을 경우, 이 임계 비율이 0.5 라는 것은 이미 수학자 해리 케스튼 (Harry Kesten) 에 의해 증명되었어.
이런 임계 현상은 스웨덴의 코로나 방역에서 언급된 집단 면역과 큰 관련이 있어. 어떤 집단의 사람들 중에 N명은 면역이 있을 거라고 가정하고 (면역력이 약한 사람들은 먼저 죽어나가고......(?)) 살아남은 사람들 그리고 이미 걸려서, 혹은 다른 이유로 새로이 면역력을 갖게 된 사람들에게 면역력이 충분히 있다면, 언젠가는 면역성을 가진 사람의 비율이 임계 비율 이상이 되기 때문에(??) 사회의 구성원들은 자정적으로 살아남는다(???)는 내용이야.
하지만 수학 이론을 실제 세계에 적용하려면 많은 제약이 따르는데, 앞서 언급한 가정에서도 모순을 찾아 볼 수 있어.
1. 시간이 지나도 전염병이 변이를 일으키지 않을...까?
2. 시간이 지나도 전염성은 일정한 성질을 가질...까?
생물학적으로, 생물은 진화하고 환경에 따라 변이를 일으켜. 따라서 변이를 일으키기 전의 바이러스에는 면역이 있을 지 몰라도, 변이가 일어난 후의 바이러스에 면역이 없다면, 그 사람은 새로운 변종 코로나 바이러스에 감염될거야.
또한, 소개 했던 침투 이론에서 말하는 이차원 격자 위에 있는 점 들이야 이동도 하지 않고, 제자리에 있고, 이 점들을 연결하는 선들의 정보는 항상 같아, 즉 상수이지. 하지만 사회를 이런 격자 위의 점으로 보기엔 좀 무리가 있어. 어떤 예상하지 못한 이벤트가 일어나지. (예를 들면, 어떤 예상치 못한 집회가 생기고, 연말 송년회 행사들이 있고 등). 따라서, 사회 현상을 수학적으로 모델링 하는 것이 말처럼 쉽지는 않아. 쉽지 않기 때문에 역학이라는 학문이 있는 것이기도 해.
오늘은 방구석에서 공포감에 더더더..덜덜... 떨면서 한번 코로나와 침투 이론, 그리고 집단 면역에 대한 내용을 소개해 봤어. 다들 손을 잘 씻고, 스스로 주의하여 코로나에서 멀어지자. 다음에 돌아올게. 이 글에 대한 피드백은 댓글이나 인스타그램 DM으로 줘 :)




의견을 남겨주세요
프레드
전염병 전파 시뮬레이션 연구들은 2d lattice보단 mean field approach를 더 많이 사용할겁니당
프레드
스웨덴이 집단 면역 전략을 사용했다는 건 논란의 여지가 있습니다. 전략이라기보단 포기(?)죠. (https://www.hankookilbo.com/News/Read/A2020102611120000132) 역학자분들이 집단 면역은 [전략]이 아니라고 말씀하시던데, 저는 (어떤 면에선)전략으로서 가능하다고는 생각합니다. 집단면역이 '전략'으로서 작용하려면 목표를 감염률 낮추기가 아니라 총 사망자수 낮추기가 되어야 합니다. 1. 취약 계층의 사회 교류를 완전히 차단하고 건강하고 죽지 않을 사람들간에 의도적으로 감염을 일으켜 면역을 형성시킵니다. 2. 면역된 사람들의 숫자가 threshold를 넘어가면 취약계층의 사회 교류를 재개합니다. 이렇게 되면 노인 등의 취약계층이 감염될 위험이 적어지겠죠. 물론 현실적인 방법은 아닙니다. 위험군이 아닌 40~50대 covid 사망률도 0.1%이상이라 너무 높고, 도달해야하는 threshold도 국민의 수십%이기 때문이죠.
화장실에서 읽는 과학과 수학
안녕하세요! 자세한 코멘트 감사드립니다 :) 2D lattice 는 '과연 침투이론이 수학적으로 증명되었는가?', '임계 현상이 실제로 수학적으로 존재하는가?' 를 언급하기 위해 증명된 예를 글에서 소개했는데, 말씀대로 코로나에 대한 연구나 전염병에 대한 직접적인 연구와 큰 상관은 없습니다. 1. 집단 면역을 전략으로 볼 수 있는가? 국가마다 다른 코로나에 대응하기 위한 다른 정책들을 사용하고, 이를 위 글에서는 전략과 같은 맥락으로 설명되었습니다. 코멘트의 링크에서 소개된, 역학 연구자 Anders Tegnell 의 인터뷰 내용을 링크로 달아드립니다. (https://www.bloomberg.com/news/articles/2020-12-01/sweden-s-top-epidemiologist-says-herd-immunity-remains-a-mystery) 여기서도 strategy 라는 용어를 사용하며, 스웨덴에서는 정확히 'Herd immunity 와 관련된 전략을 시행한다.' 라고 못박았다기 보단 '자연적인 면역 효과(저항성)를 고려하여, 코로나 바이러스의 전염은 자연적으로 제한될 것으로 기대한다.' 라는 문장을 사용합니다. (Though Sweden never targeted herd immunity as a declared strategy, officials made clear they expected some form of resistance to build in the population that would limit the spread of Covid-19.) 2. 소개하신 링크에선 집단 면역이 꼭 의도적인 감염을 통한 면역 형성이 아니라, 백신을 투여하는 방법으로 인한 면역 형성도 소개하고 있습니다. 이런 방법으로 접근한다면, 제안하신 방법이 과연 비현실적일까요?! + 덧붙이자면... Herd immunity comes when enough people in a community have either been infected or vaccinated, and are thus immune. For Covid, the percentage is estimated to range from 55% to 82%. 여기서 임계 비율은 약 55~82 % 로 예측하고 있습니다.
의견을 남겨주세요