
🎄크리스마스🎄와 연말이 다가오고 있는 요즘, 번화가에서 형형색색 불이 켜진 트리를 보기 쉬운데 말야. 그 불빛도 너무 예쁘지만, 자세히 나무를 살펴보면, 나뭇 가지에서 어떤 규칙성을 찾아볼 수 있어. 한번, 아래 사진처럼 나뭇가지가 확연히 보이는 사진을 볼까?


자연에서 찾는 규칙성
작은 잎이나 가지를 가지가 굵은 부분에서 보는 모습과 가지가 얇은 부분에서 보는 모습이 어떻게 다를까? 큰 가지에서 작은 가지로 나뉘어지고, 그 가지에서 다시 얇은 여러 가지로 나뉘어지고, 다시 얇은 가지에선 더 얇은 가지로 나뉘어져. 이런 반복되는 양상은 나무 뿐만 아니라 하늘에서 떨어지는 번개, 여러 물줄기로 나뉘어지는 강, 피요르드 해안선 등 자연의 여러 부분에서 발견돼.
이처럼, 수학적으로 작은 일부 부분이 전체와 비슷한 모습으로 반복되는 양상 혹은 그 구조를 프랙탈(Fractal) 이라고 해. 특히, 프랙탈에서는 자기유사성(Self-similarity, 혹은 자기 닮음) 이라는 특수한 성질을 가져. 이를 좀더 그림으로 좀더 쉽게 설명해 보자면, 아래 그림과 같아.

이 프랙탈이라는 용어는, 어떤 수학자에 의해 이름 붙여지고 해석되었어. 그는 브누아 망델브로(Benoit Mandelbrot)인데, 그가 쓴 자연에서 프랙탈 구조(The Fractal Geometry of Nature) 라는 글에서 처음 시작됐어. 망델브로는 부서지기 쉬운, 부러진이라는 어원을 가진 라틴어 fractus 을 따 와서 fractal 이라는 이름을 지었어.
망델브로는 프랙탈을 어떤 점화식을 이용한 수의 집합으로 표현했고, 이 수의 집합을 망델브로 집합이라고 해. 점화식이란 건 간단하게 예를 들어 말하자면, 어떤 n번째 수와 n+1번째 수의 규칙을 만들어서 나타낸 것과 같은 수학적 식을 말해. 망델브로 집합 뿐만 아니라, 여러 다른 점화식으로 이를 표현한 칸토어 집합, 줄리아 집합 등 각 점화식, 즉 프랙탈이 만들어지는 규칙에 따라 다양한 프랙탈이 만들어 질 수 있어.


프랙탈은 우리 몸에서도
아까 프랙탈은 자연에서 찾아볼 수 있다고 했잖아. 즉, 자연에서 만들어진 우리 몸에서도 이런 프랙탈 구조를 찾아볼 수 있어.
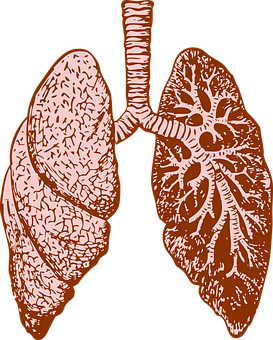
폐는 폐포라고 불리는 작은 포도송이 모양의 부분으로 이루어져 있어. 무수히 많은 폐포들이 폐의 한 부분을 이루게 돼. 목과 코에서 부터 통하는 기관지로부터 폐포에 이르기까지 공기의 통로는 큰 가지에서 작은 가지를 뻗치는 것 처럼 반복적으로 뻗어나가는데, 이 또한 프랙탈의 구조를 띠고 있어. 몸을 이루는 혈관의 경우, 특히 동맥에서 모세혈관으로 뻗을 때 까지 보이는 모습 또한 이런 프랙탈의 모습을 띠지. 뇌의 표면에는 무수히 많은 주름이 있는데, 커다란 주름에서 잔주름으로 계속되어 반복되어 나가. 이 또한 프랙탈의 예지. 이와 같이, 폐, 혈관, 뇌에서 볼 수 있듯이 어떤 표면적을 넓히면 이점을 갖는 구조에서 프랙탈의 구조가 유용하게 쓰이는 것을 확인할 수 있어.
오늘은 크리스마스 트리에서 부터 확인할 수 있는 프랙탈의 구조를 한번 알아봤어. 이에 관련된 더욱 자세한 수학적 내용은, 유료 구독자에게 따로 제공 될 예정이야.
지금까지 약 삼개월 가량 메일리 뉴스레터를 진행하면서 여러 주제 - 유명하지 않은 과학자&수학자들, 영화에서 들어본 과학, 알고리즘 - 와 관련된 글을 썼고, 각 주제와 관련된 마침글 또한 쓰여지기도 했어. 물론 그 중에 지금도 발행이 준비 중인 것도 있어. 2021년을 맞이하면서, 새 글을 쓰기 전에 약 2주 정도 뉴스레터 발행을 쉬고 새 글을 준비하고 다듬는 시간을 가지려 해. 쉬는 동안 뉴스레터의 진행 방향 또한 되짚어 보려고 하기도 하고. 그럼, 모두 새로운 글로 2021년에 다시 찾아올게. Merry Christmas and Happy New Year!





의견을 남겨주세요