유명한 사람들의 유명하지 않은 사실들

이런 차나 코코아 가루를 물에 타서 먹을 때 숟가락으로 회오리를 만들어 본 적 있지? 과학자들은 차를 마시면서 이 회오리와 찻잎을 보며 어떤 의문을 가졌어. 왠지 기존의 과학적 이론에 근거하면 그러면 안될거 같은데 찻잔속에선 그런 일이 일어났단 말이야? 그 의문은 바로 '왜 찻잎은 회오리 바깥으로 퍼지는게 아니라 가운데로 뭉칠까?' 였어. 

기존 과학자들의 생각은 다음과 같아. 우리가 원심력이라는 단어를 들어본 기억이 어렴풋이 있을거야. 그렇지?! 쉽게 생각해보면 쥐불놀이나, 혹은 물을 넣은 양동이를 사람이 팔로 풍차처럼 돌리면 물이 떨어지지 않는 예시를 떠올려 보면 될거야. 물이 양동이 바닥에서 떨어지지 않게 회전 반경인 원의 바깥방향으로 향하는 힘 = 원심력! 이라고 생각하면 돼! 

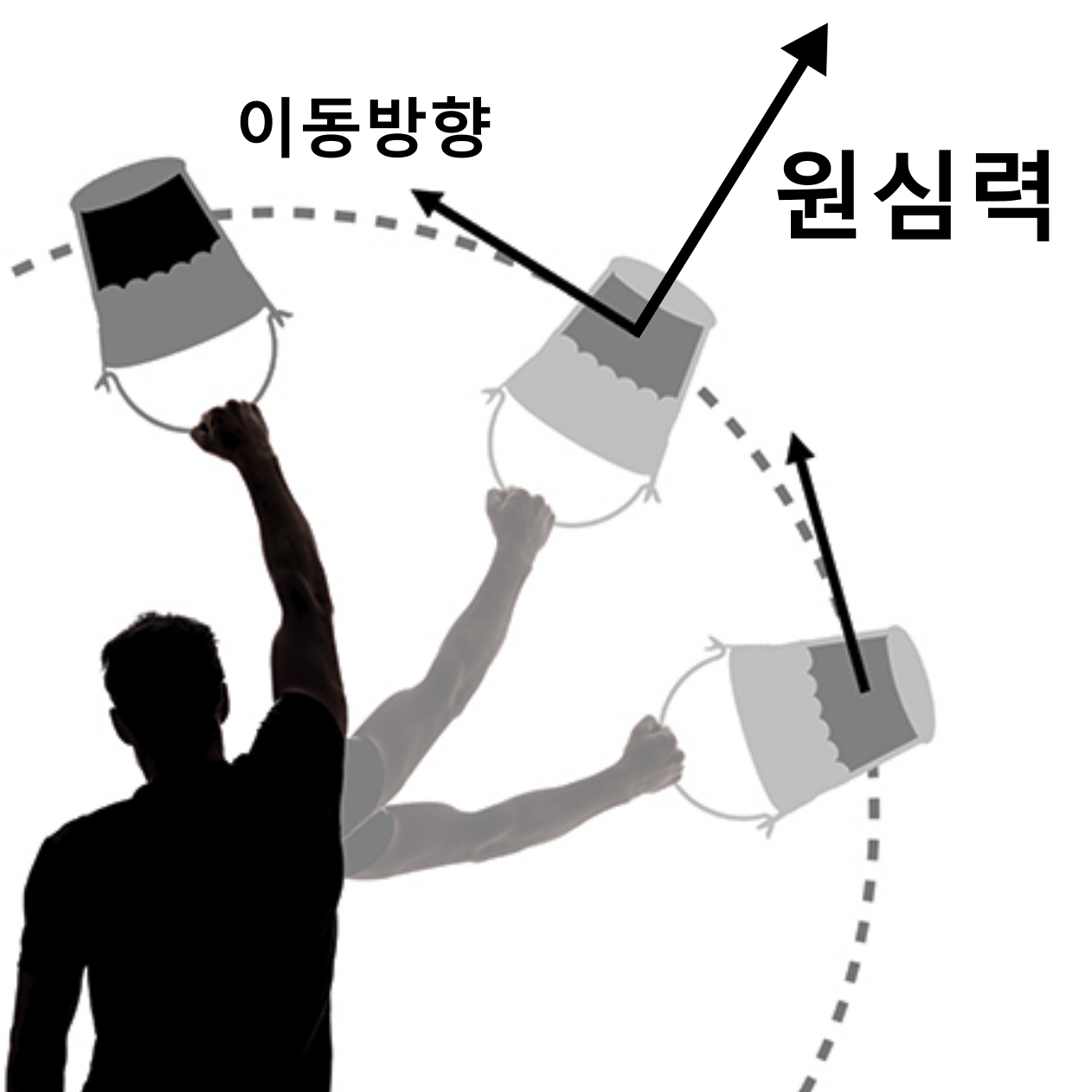
그럼 아까 말한 찻잔을 다시 가져와볼게. 만약 찻잔에서 물이 회전해서 원심력이 생긴다면, 찻잎들은 원의 바깥 방향, 즉 찻잔의 벽 방향으로 이동하려고 할거야. 그럼 차를 숟가락으로 저으면 찻잎들이 찻잔에 줄지어 붙어있는게 맞겠지? 하지만 왜 가운데에 모여있는 걸까? 

이와 같은 현상을 발견한 과학자들은, 이를 '찻잎 역설 (Tea leaf paradox)' 이라고 불렀어. 그리고 한 과학자의 논문을 통해 찻잎 역설은 이론적으로 증명이 돼. 그의 이론에 의하면, 찻잎은 원심력 때문에 이동할 수 있는 것은 맞아. 하지만, 물의 회전으로 인한 물과 잔 표면의 마찰력 또한 언급했어. 이 마찰력이 만약에 원심력보다 크면 (원심력 < 마찰력), 찻잎은 가운데로 모이게 돼.   

이 해결법을 제시한 사람은 상대성 이론, E = mc2 (엠씨스퀘어) 나 브라운 운동, 양자역학의 불완전성 등으로 유명한 알베르트 아인슈타인이야!  

아인슈타인의 찻잎 역설과 관련된 논문은 76회 인용되었어. 아인슈타인의 논문 중에 EPR 역설이라 불리는 (저자인 Albert Einstein, Boris Podolsky, Nathan Rosen 세 명의 앞 글자) 논문은 19573회 인용이 되었는데, 참 차이가 크지! 이 EPR 역설의 경우는, 그 당시 뜨거운 감자 🥔 였어. 왜냐하면 지금은 받아들여지는 양자역학이라는 학문이 그 당시엔 정립되지 않아 이러쿵 저러쿵 말이 많았거든. EPR 역설도 양자역학을 신랄하게 까내리는 논문이었어. 

오늘 엠씨스퀘어! 상대성이론! 빛의 속도! 가 떠오르는 아인슈타인의 TMI 를 알아봤어. 아인슈타인 하면 실생활에서는 찾기 어려운 복잡한 이론물리학만 공부한 사람인 줄 알았는데, 찻잔 속 물리세계도 궁금해 한 사람이었나봐! 다음 주에는 통계학 그리고 데이터 시각화에 관련된 내용으로 다시 찾아올게!  

매주, 매월, 글을 받아보고 싶다면? 👉🏻 구독자가 되어주세요!
읽고 싶은 주제가 있나요? Instagram DM으로 알려주세요! 👉🏻 @the_toilet_papers