금융에서의 자동 미분 (채권 트레이더, 이유성)

CDFi 2기 5번째 세션 <2>

hosted by 이유성 (채권 트레이더)
월스트리트 디파이의 세미나 내용은 유튜브에서 영상으로도 보실 수 있습니다.

“자동미분 기술은 시뮬레이션 기반 모델의 불안정성과 과도한 비용 추가 없이 실시간으로 정확한 리스크 계산을 제공합니다.”
— 이유성, CDFi 세미나

🧠이번 세션 주제

이번 CDFi 세미나에서 이유성님은 자동미분(Automatic Differentiation, AD)이라는 강력한 수학적 도구와 이를 금융 리스크 모델링에 실무적으로 적용하는 방법에 대해 소개해주셨습니다. 기초 수학 개념에서부터 실제 시장 적용 사례에 이르기까지, AD가 현대 금융의 pricing engines과 calibration system을 어떻게 혁신하는지 알아보고자 합니다.

🔍 금융에서 리스크가 중요한 이유

모든 거래 및 투자 결정은 한 가지 필수적인 입력값에 의존하는데, 그것이 바로 리스크입니다. 주식 파생상품이든, 채권이든, 금리 상품이든 간에 금융 기관은 시장 변수의 변화에 따라 가격이 어떻게 달라지는지를 정확히 파악해야 합니다. 그렇다면 리스크를 어떻게 계산할까요?

일부 금융상품은 닫힌 해석해(closed-form solution)를 갖습니다. (예: Vanilla Option)
반면, 모기지 포트폴리오나 Exotic Option(이국적 옵션)과 같은 복잡한 상품은 시뮬레이션이나 유한차분(finite difference) 등 수치적 방법을 필요로 합니다.

⚠️ 병목 지점: 유한차분(Finite Difference) 방식

전통적인 ‘범프 앤 이밸(Bump-and-Eval)’ 접근법은 변수 값을 소폭 변경한 뒤 가격 모델을 재실행하여 도함수를 근사합니다. 즉, x값을 0.1만큼 변경했을 때 y값이 얼마나 변하는지를 측정하여 기울기(변동성;리스크)를 근사합니다.

한계점:

❗ 아주 작은 스텝 또는 큰 스텝에서 발생하는 수치적 불안정성이 존재합니다.
🧮 파라미터 수가 많을수록 연산 비용이 급증합니다.
🚫 경계 근처에서의 부정확성(현실 세계의 프라이싱 모델에서 흔히 관찰됨)이 존재합니다.

⚙️ 해결책: 자동미분(Automatic Differentiation, AD)

자동미분(AD)은 함수의 실행과 동시에 정확한 도함수를 계산하여 위의 문제들을 해결할 수 있습니다.

🔄 자동미분의 두 가지 모드:

1. 순방향 모드(Forward Mode)

입력에서 출력으로 도함수를 전파합니다.
입력 수가 적고 출력이 많은 경우에 효율적입니다. ✔

2. 역방향 모드(Backward Mode, Adjoint)

출력에서 입력으로 도함수를 역산합니다.
입력 수가 많고 출력이 하나인 경우에 효율적입니다. ✔

💡 자동미분은금융 프라이싱 모델뿐만 아니라 딥러닝에서도 핵심적인 계산 역량을 제공하곤 합니다.

💡 이원수(Dual Numbers)가 자동미분을 작동하게 하는 원리

순방향(Forward-Mode) 자동미분은 이원수(Dual Number)를 사용합니다.

x + aε where ε² = 0, but ε ≠ 0

이 기법은 함수와 그 도함수를 한 번에 평가할 수 있도록 합니다. ) 함수의 값과 기울기(미분값)를 동시에 계산할 수 있게 해주는 영리한 수학적 지름길입니다. 보통 컴퓨터는 함수가 어떻게 변하는지 알아내기 위해 입력값을 조금씩 바꿔가며 여러 번 실행해야 하는데, 이는 느리고 비효율적입니다. 하지만 듀얼 넘버는 입력에 ε이라는 특별한 “허수 같은 꼬리표”를 붙이는데, 여기서 ε² = 0이 됩니다. 이 트릭 덕분에 함수를 한 번만 계산해도 결과값과 변화율을 함께 얻을 수 있습니다. 실제로 이런 방식은 금융 리스크 시뮬레이션 같은 복잡한 계산을 훨씬 더 빠르고 정확하게 만들어 줍니다.

🔎 Henrard(2011)가 언급한 자동미분의 효율성전통적 시뮬레이션 ≈ 70–80회자동미분(AD) ≈ 4–5회

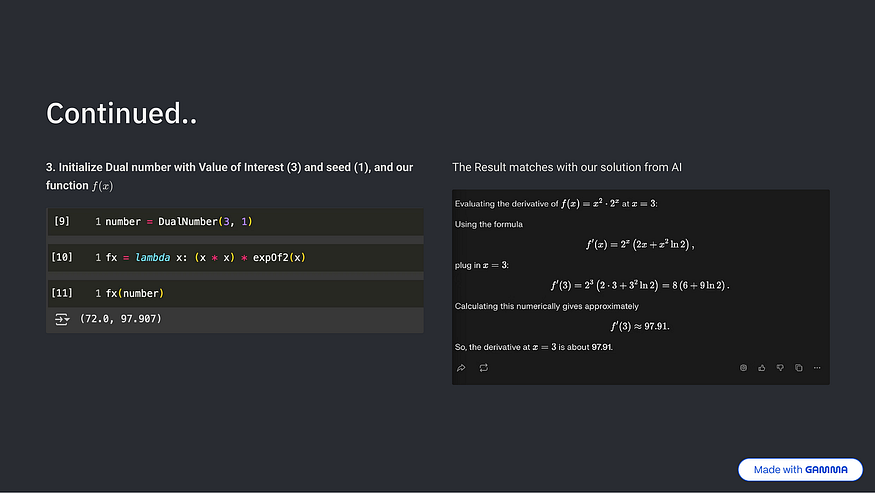
🧪 실습해보기

이유성님께서 이원수를 직접 설정하고 Python으로 자동미분을 구현해볼 수 있는 실습용 Google Colab notebook 링크를 공유해주셨습니다.

📈 실제 금융 적용 사례

자동미분(AD)은 정량 금융 및 리스크 분석 전반에서 표준 도구로 사용되고 있습니다.

📉 몬테카를로 시뮬레이션에서의 그릭스 계산(Giles & Glasserman, 2005 — “Smoking Adjoints”)
💹 금리 시장 시뮬레이션(현재는 사용하지 않는 LIBOR 모델 포함)
🔗 상관관계 리스크 및 구간화(Binning)
🧮 암시함수정리(Implicit Function Theorem)를 이용한 모델 캘리브레이션(수익률 곡선 및 프라이싱 모델 최적화에 사용)

🏦 Sell-Side vs. Buy-Side 영향

Sell-Side(예: 투자은행)→ 고객 실행을 위한 빠르고 정확한 가격 책정을 우선시 함→ 빠른 실시간 호가 제공 능력 따라 수수료 수입이 달라짐
Buy-Side(예: 헤지펀드, 자산운용사)→ 리스크와 향후 가격 변화를 예측하는 데 집중함→ AD는 미래 민감도를 효율적으로 모델링함으로써 더 나은 트레이딩 의사결정을 가능하게 함