2주에 한번씩 과학과 관련한 다양한 이야기를 받아보고 싶으시다면? 구독은 큰 힘이 됩니다. :)
스몰레터 에디터 올림
구독자님, 1에서 9까지의 수에서 가운데에 있는 숫자를 떠올려보세요. 아마도 5나 4를 떠올리셨을 겁니다. 하지만 여기서 흥미로운 사실 하나, 아직 숫자를 제대로 배우지 않은 어린 아이들이나, 현대 문명과의 접촉이 많지 않은 사회권의 사람들에게 이 질문을 하면 3이라는 대답이 많이 나온다고 합니다. 연구에 의하면 인간이 숫자를 생각할때, 우리는 주로 1, 2, 3, 4, 처럼 선형의 구조가 아니라 로그의 구조에 더욱 가깝게 생각한다고 합니다. 3의 0승은 1이고, 3의 2승은 9니까, 1과 9 가운데의 숫자를 고르라면 3의 1승, 3을 고른다는 것이죠.
🧐 로그가 뭐더라... 가물가물한데...
로그 그리고 로그함수, 고등학교 이후로는 들어본 기억도 없는 것 같은, 없이 살아도 인생에 전혀 지장 없는 이 개념을 우리가 사실은 자연스레 생각하며 산다니, 조금은 의아한 부분입니다. (안타깝지만) 잠시 고등학교 수학 시간으로 돌아가 로그함수를 살짝 복습해 볼까요?
로그 함수는 지수함수의 역함수 입니다. (갑자기 고등학교 수학시간의 악몽이 떠오르는 문장이죠?) 2를 4번 곱하면 16이죠. 그러면 2를 몇번 곱해야 16이 되는가, 그 역산의 과정이 로그입니다.
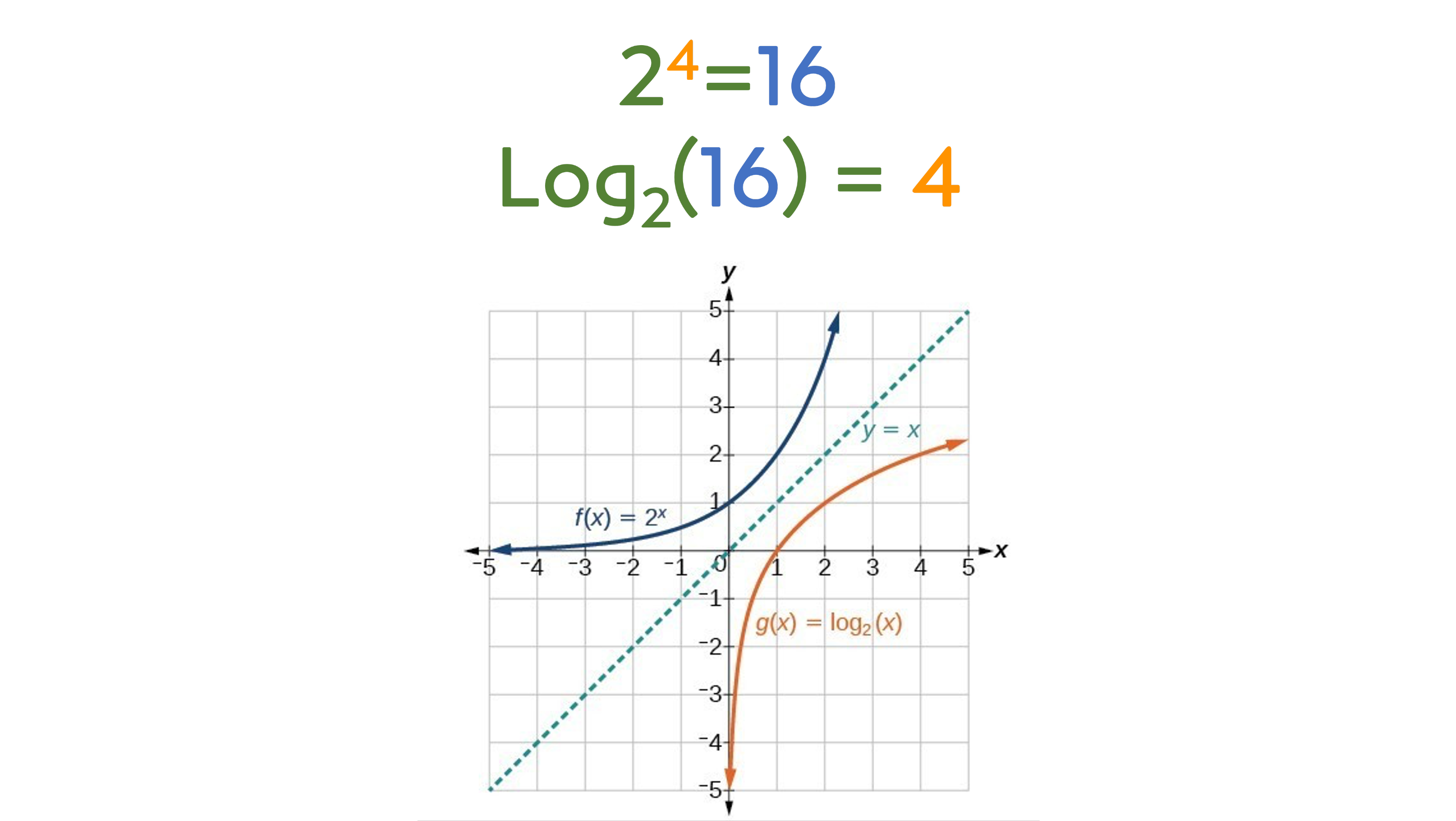
말로만 하면 재미 없으니까 그래프로도 그려보죠. 2의 지수함수의 그래프와 log2 함수의 그래프는 y=x 인 선을 기준으로 대칭인 모양을 하고 있습니다. 지수함수의 그래프는 x=0 이상의 값에서 그야말로 기하급수적으로 늘어나지만, 로그함수의 기울기는 계속 상승세지만 점점 완만해 집니다. 즉, 숫자가 커질 수록, 그 숫자의 로그 값은 천천히 늘어나는 것이죠.
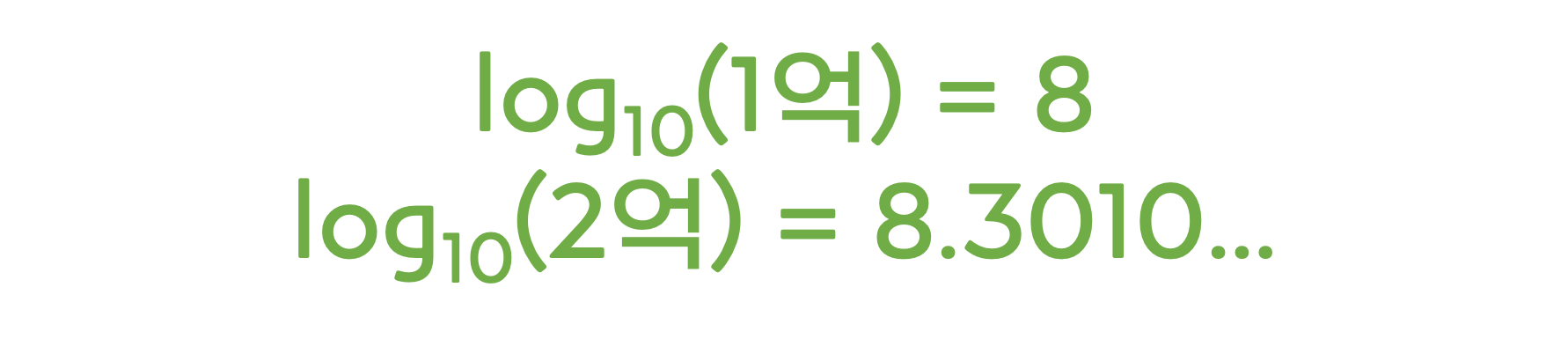
🥂 이 조명, 온도, 습도... 그리고 로그
그럼 우리가 대체 어떻게 로그 구조로 생각을 한다는 걸까요?
우선은 우리의 감각부터가 그렇습니다. 양손에 한 쪽에는 200그램, 다른 쪽에는 220그램의 물건을 들고 있다고 생각해보세요. 이 20그램의 차이가 느껴진다고 가정해볼게요. 그러면 이번에는 한쪽에는 1킬로그램, 다른쪽에는 1.02 킬로그램인 아령을 들고있다고 생각해봅시다. 둘의 무게 차이는 똑같이 20그램입니다. 하지만 후자에서는 그 차이가 거의 느껴지지 않을겁니다. 우리는 자극의 변화를 절대적으로 느끼기보다 상대적으로 느낍니다. 이게 바로 베버-페흐너의 법칙인데요, 페흐너는 이 현상을 아주 다음과 같이 표현합니다: "감각의 정도는 가해지는 에너지의 크기의 로그값이 증가할 때 비례해서 증가한다."
이 현상은 우리 주변에서도 많이 찾아볼 수 있는데요, "도시는 무엇으로 사는가"와 알쓸신잡의 패널로 유명한 건축가 유현준님은 "왜 고층 건물은 많아졌는데 63빌딩만큼의 임팩트는 없는걸까요?" 라는 질문에 당시의 건물들 중 가장 높았던 건물이 30층짜리 건물이었다는 사실에 주목합니다. 다른 건물들에 비해 2배 이상 높아진 건물이 등장한 거죠. 그리고 63빌딩 이후 지어진 70층, 80층의 건물들이 63빌딩만큼 충격적이지 않듯이, 절대적인 건물의 높이가 얼마나 증가했나보다 새로운 건물의 높이가 상대적으로 몇배 증가했느냐가 우리가 느끼는 높이 감각에 더 큰 영향을 미친다고 이야기 합니다.

(이미지 출처: 경향신문)
우리의 인식도 마찬가지입니다. 2010년에 파리 시립 대학 등에서 수학적 사고가 발달된 성인을 대상으로 한 실험을 진행했는데요, 이들을 대상으로 무작위로 선정된 숫자들을 일직선상에 표시하라고 했을 때 이들은 전부 수학적으로 정확하게 표기를 했다고 합니다. 하지만 이들에게 숫자가 아니라 세기 어려운 촘촘한 점 이미지가 주어졌을 때, 참가자들은 점의 개수가 많은 이미지들은 로그값이 비슷한 이미지들끼리 하나의 그룹으로 묶어버리는 경향을 보였다고 합니다. 200개와 250개의 점을 한 그룹에, 1000개와 1200개의 점을 한 그룹에, 이를 비슷한 범위의 숫자로 생각했다는 것이죠. 전문가들은 이를 Compression Effect, 압축 효과라고 부릅니다.
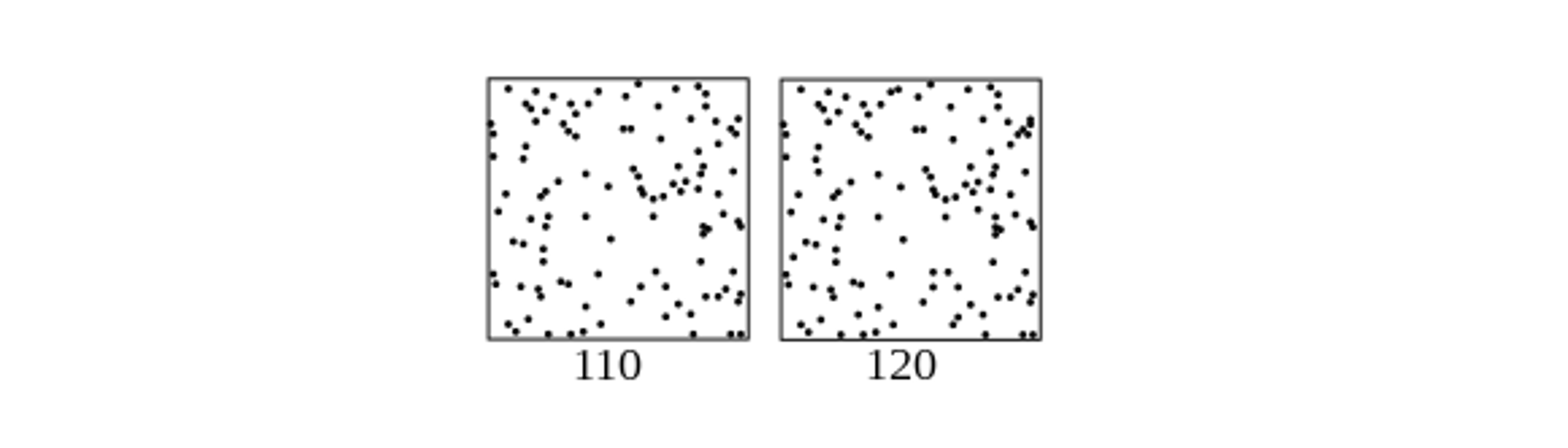
(이미지 출처: 위키피디아)
저 역시도 최근에 비슷한 경험을 했는데요, 한 기사에서 달에서 발견 된 암석을 조사해봤더니 달의 나이가 사실은 44억 2천만년이 아니라 44억 6천만년 정도로 새로이 예측됐다는 내용을 읽었습니다. 그리곤 생각했죠. 그 전 값도 비슷한데? 하지만 인류의 역사가 6천년 정도임을 생각하면 4천만년은 정말 정말 정말 오랜 시간입니다. 하지만 우리의 뇌는 그 크기의 차이를 절대적으로 인지하지 않고, 두 값을 비슷한 범위의 숫자로 생각하곤 하죠.
🧠 우리의 뇌는 왜 그러는 걸까?

(이미지 출처: 프리픽)
우리가 왜 이렇게 숫자나 감각등을 압축해서 기억하는가에 대해선 아직 다양한 이론이 제기되고 있습니다. 그렇지만 그 중에서 가장 설득력 있는 이론은 생존을 위한 최적화라는 점입니다. 우리가 숫자 정보를 기억할 때 최소화 해야하는 오류는 상대적인 오류이지, 절대적인 오류가 아니라는 겁니다. 저쪽 초원으로 가면 사자가 5마리였는지 6마리였는지 가물가물하다 쳐도 크게 대세에 지장이 없습니다만, 사자가 5마리였는지 50마리였는지를 잘못 기억한다면 큰일난다는 거죠. 즉 상대적인 크기를 더 중요하게 생각하도록 진화한 겁니다.





![[모두를 위한 우주 2편] Omnibus Ad Astra- 우리는 모두 우주에 간다의 썸네일 이미지](https://cdn.maily.so/202309/1694991718437314.jpeg)

![[모두를 위한 우주- 3편] 대화가 필요해 - 외계인과의 조우를 상상하기의 썸네일 이미지](https://cdn.maily.so/202309/1695341713487677.jpeg)


의견을 남겨주세요