수학은 항상 아름답기만 하진 않습니다

수학의 아름다움을 이야기하는 글은 찾아보기 어렵지 않습니다. 아름다운 수식을 바라볼 때 뇌의 반응과 예술품을 볼 때 뇌의 반응이 유사하다는 연구 결과도 있었습니다.

하지만 수학이 항상 아름답고 우아하기만 한 것은 아닙니다. 수학이 추해 보일 때에 대해서는 사람들이 잘 말하지 않는 것 같습니다(이미 이미지가 안 좋기 때문일까요?). 오늘은 수학이 전혀 아름다워 보이지 않는 두 사례를 준비했습니다.

‘4색문제’는 위상수학의 문제로, 지도 상에서 서로 인접한 나라들을 서로 다른 색으로 칠해 구분할 수 있게 하되 4개의 색깔만을 써서 칠할 수 있겠는가 하는 문제입니다. 제가 수학과에서 공부를 할 때 위상수학 과목은 지극히 추상적이어서 어렵기도 하면서 재밌고, 아름다운 증명도 많은 과목이었습니다. 4색문제도 아주 아름답게 증명될 것만 같은 느낌이 나는데, 이 문제는 아주 아름답지 못한 방법으로 이미 증명이 되었습니다.

4색으로 칠한 미국 지도

독일의 헤쉬는 4색문제에서 나올 수 있는 지도의 유형을 약 9천 개 정도로 정리했습니다. 이후 미국의 하켄과 아펠은 이 유형을 1936개까지 줄여냈습니다. 그리고 컴퓨터를 이용해 이 1936개의 유형 하나하나를 4색으로 칠하는 것이 가능함을 증명했습니다. 이 자료를 바탕으로 아들, 딸을 시켜 직접 지도를 하나하나 칠하게 하는 것으로 논문은 완성되었습니다. 이 논문의 첫 장엔 ‘아들, 딸에게 감사하다’라는 내용이 있습니다.

그래도 4색문제는 ‘언젠가 1936개의 경우를 노가다로 풀어내는 것보단 아름다운 증명이 나올 수도 있지 않을까’라는 기대가 남아 있습니다. 하지만 Square packing 문제는 언젠가 아름다운 풀이가 나오리라는 기대도 어려워 보입니다.

4개의 정사각형을 1개의 큰 정사각형 안에 집어넣는 것을 생각해 봅시다. 이 때 1개의 큰 정사각형을 최대한 작게 만드는 방법은, 작은 정사각형을 2x2 형태로 배치하는 것입니다. 이렇게 n개의 정사각형을 감싸는 가장 작은 정사각형을 찾는 문제가 Square packing 문제입니다.

4개나 9개 같은 경우에는 문제가 쉬워 보이지만, 17개의 정사각형을 감싸는 정사각형은 어떤가요? 풀기가 쉽지는 않아 보입니다. 아래와 같은 형태로 17개의 정사각형을 배치하면 꽤나 아름다워 보이고 여백도 적어 보입니다.

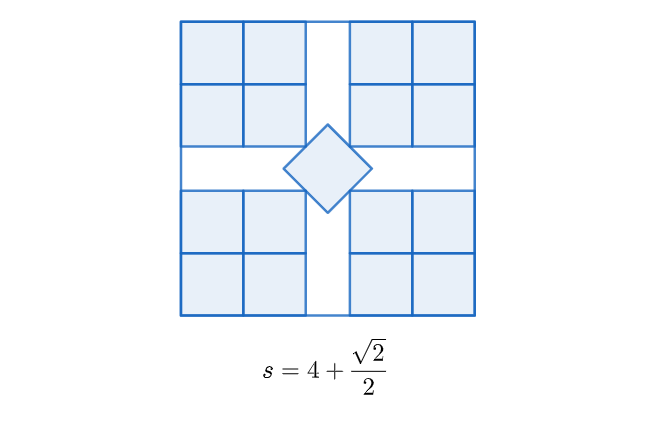
하지만 충격적이게도, 다음의 추한 형태로 17개의 정사각형을 쑤셔 넣었을 때 위의 배치보다 더 효율적인 배치가 가능합니다.

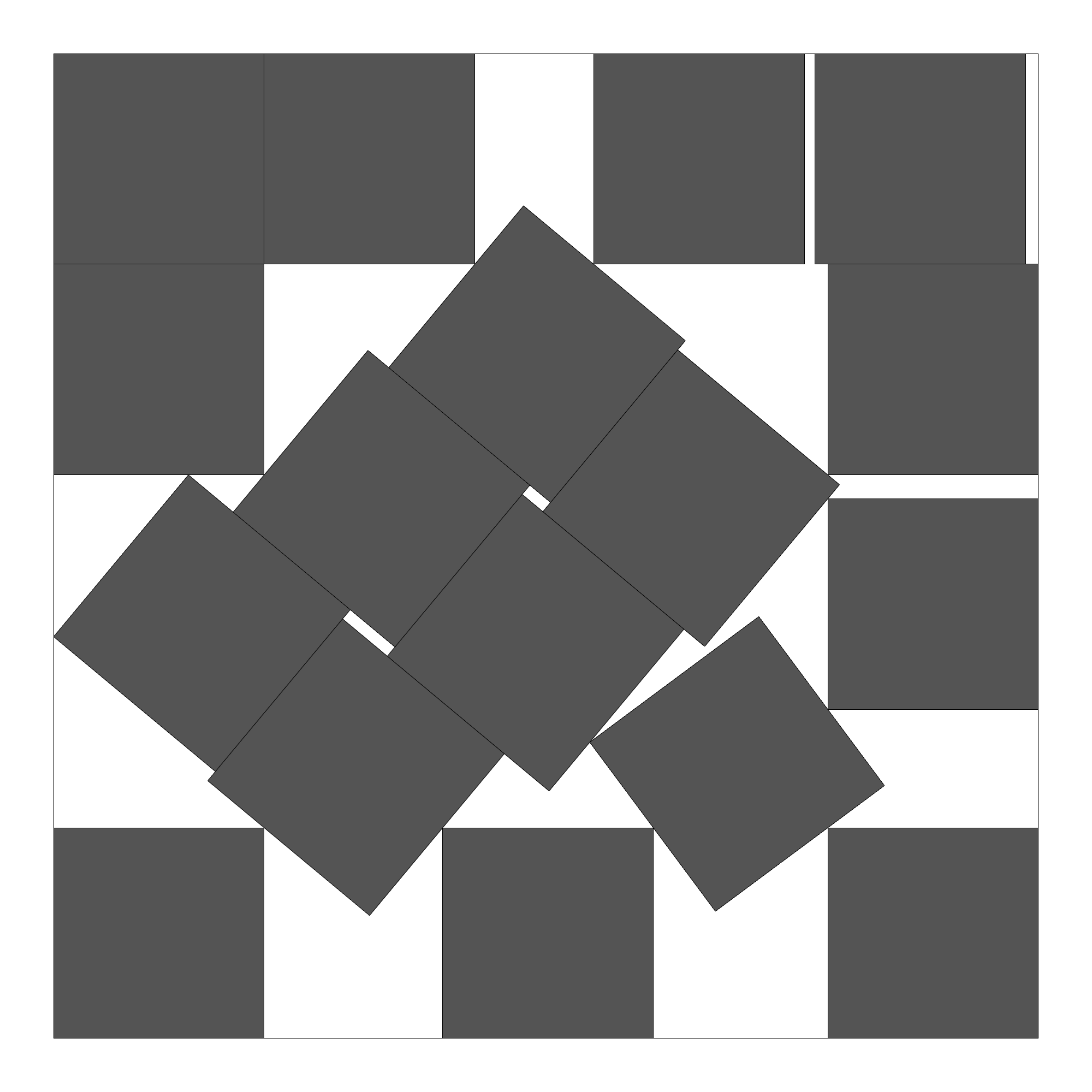
아직 이 형태가 17개의 정사각형을 감싸는 가장 작은 정사각형이라고 증명되진 않았지만, 밝혀진 것 중엔 가장 작습니다. 저는 처음 이것을 보았을 때 경악을 금치 못했습니다. 수학문제의 해답이 저렇게 못생기게 나오는 경우는 한 번도 보지 못했기 때문입니다. 혹시 물건을 쑤셔 박는 버릇이 있어 잔소리를 듣는 편이라면, 앞으로는 ‘어쩌면 이게 수학적으로 더 나은 방법일 수도 있어’라고 변명을 해 봅시다.