원은 가장 익숙한 곡선입니다. 그래서 깊게 생각해 보지 않았다면 곡선으로 이루어진 많은 것들을 원(또는 그 일부인 호)이겠거니 생각하기 쉽습니다. 하지만 세상엔 다양한 종류의 곡선이 있고, 그 곡선들은 원이 해내지 못하는 일을 해냅니다.
고속도로나 철도의 커브길을 만든다고 생각해 봅시다. 북쪽을 향해 가다가 동쪽으로 방향을 트는 길을 만든다면 가장 먼저 떠오르는 방법은 사분원 모양으로 도로를 휘는 것입니다. 하지만 이렇게 원의 형태로 커브길을 만들면 큰 문제가 생깁니다.
학창 시절 과학 시간에 배웠을 내용을 잠시 떠올려 봅시다. 움직이는 물체가 아무 힘을 받지 않으면 직선으로 움직입니다. 움직이는 물체가 계속해서 움직이는 방향에 수직으로 힘을 받으면 원을 따라 움직입니다. 따라서 반듯하게 가다가 사분원 커브길을 돌려면, 핸들을 반듯하게 놓고 달리다가 커브길에 들어서는 순간 갑자기 핸들을 크게 꺾어야 합니다. 승객들 또한 좌우로 받는 힘이 0이다가 커브를 도는 순간 확 힘을 받게 됩니다.
이 문제를 해결하기 위해 도로와 철도 설계자들은 '클로소이드(Clothoid)'라는 특별한 곡선을 사용합니다. 클로소이드는 진행방향에 수직으로 가하는 힘을 0에서부터 서서히 올렸을 때 얻을 수 있는 곡선입니다. 이 형태로 커브길을 만들면 자동차나 열차가 직선 구간에서 곡선 구간으로 진입할 때, 운전자가 핸들을 점진적으로 돌리면서 자연스럽게 곡선 궤적을 그릴 수 있습니다. 원심력이 갑자기 생기지 않고 서서히 증가하므로 승객들 또한 불편을 덜 느낍니다.
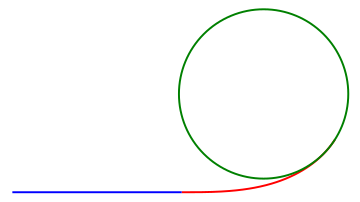
클로소이드는 1744년 레온하르트 오일러가 처음 연구해 '오일러 나선'이라는 이름도 갖고 있습니다. 철도 엔지니어들은 한참 후인 1880년대에야 이 곡선을 독자적으로 발견하고 '철도 전환 나선'이라고 불렀습니다. 오일러의 업적과 철도 엔지니어들의 발견이 연결된 것은 1922년이 되어서야 이루어졌습니다.
자연에서는 신기하게도 쥐의 수염이 클로소이드 형태를 따른다고 합니다.
미적인 이유에서 원을 피하는 경우도 있습니다. 스마트폰의 앱 아이콘들을 보면 정사각형을 기본으로 하여 끝을 원형으로 처리한 것처럼 보입니다. 앱 개발을 직업으로 하고 있는 저도 처음엔 그렇게 생각했었는데, 앱 개발 시에도 보통 이런 형태를 보면 코너에 반지름을 얼마나 줄 것인지만 정해 그려내는 경우가 많기 때문입니다.
하지만 앱 아이콘은 사실 사각형에 코너만 원형인 형태가 아니라, 반듯한 곳 없이 전체가 곡선으로 되어 있습니다. 이 곡선의 이름은 정사각형(Square)과 원(Circle)을 합쳐 스쿼클(Squircle)이라 합니다.

스쿼클은 수학적으로 '초타원(Superellipse)'의 한 종류로, 보통 다음과 같은 방정식으로 표현됩니다:
|x|^4 + |y|^4 = r^4
일반적인 원의 방정식이 x^2 + y^2 = r^2인 것과 차이가 있습니다.
곡선이 인간에게 좀 더 친근하고 편안한 느낌을 주기 때문에, 스쿼클은 끝만 둥글게 처리한 사각형보다도 더 부드러운 느낌을 줍니다. 애플은 앱 아이콘, 제어 항목, 키보드, 홈 버튼 등 다양한 분야에 스쿼클을 활용합니다. 안드로이드도 오레오 버전에서 적응형 아이콘 중 하나로 스쿼클을 채택했고, 삼성의 One UI도 스쿼클 형태의 아이콘을 사용합니다. 그 밖에도 접시 디자인이나 카카오톡 프로필 사진 등 다양한 곳에서 스쿼클 형태를 찾아볼 수 있습니다.
더 알아보기
페퍼노트, 기차는 어떻게 회전할 수 있을까요?
Wikipedia, Euler spiral
Wikipedia, Squircle









의견을 남겨주세요