지난 4월 19일, 페퍼노트의 구독자 수가 100명을 돌파했습니다.🎉 페퍼노트를 시작할 때, 받는 사람이 없는데 메일을 보내면 민망하니까 구독자가 10명을 넘기면 시작하겠다고 주변에 선언했었습니다. 그 때는 10명을 못 넘기면 어떡하나 조마조마했는데 약 3주의 시간만에 100명을 넘는 구독자 분들을 만나게 되어 감개무량합니다. 페퍼노트를 사랑해 주시는 구독자 님을 비롯한 모든 구독자 분들께 감사드리며, 나중에 "나 페퍼노트 구독자 100명 남짓할 때도 구독하던 사람이야"라고 자랑하실 수 있도록 무럭무럭 성장하는 페퍼노트가 되겠습니다.
구독자 100명 돌파를 기념하여 100에 관한 메일을 작성해보려 했는데 막상 100에 대해선 떠오르는 게 마땅치 않았습니다. 대신 페퍼노트의 구독자 숫자 증가를 예시로 설명하기 좋은 법칙인 '벤포드의 법칙'을 가지고 왔습니다.
벤포드의 법칙은 다양한 수치 데이터에서 수의 첫째 자리의 분포를 관찰해 보면, 첫째 자리가 작을 수록 많이 나타나더라는 내용의 법칙입니다. 예를 들어 여러 메일링 서비스의 구독자 수를 모아 보면, 맨 앞자리 숫자가 1인 경우, 2인 경우, 3인 경우 등이 모두 비슷하게 나타나야 할 것 같은데 실제로는 1인 경우가 제일 많고 9인 경우가 제일 적습니다.
사실 벤포드의 법칙은 페퍼노트에 처음 등장한 것이 아닙니다. '콜라츠 추측'에 대해 다뤘던 지난 메일에 링크된 유튜브 영상에서도 잠시 언급됩니다. 우박수들을 모아 보면 벤포드의 법칙을 따른다는 이야기였습니다. 벤포드의 법칙은 우박수 뿐만 아니라 여러 자릿수로 등장할 수 있는 수치 데이터들이 모인 곳이라면 곧잘 적용됩니다. 통장 잔고, 물건의 가격, 인구, SNS 팔로워 숫자 등 온갖 종류의 수치 데이터들을 모아보면 대부분 첫째자리가 1인 경우가 많고 9인 경우가 적습니다. 이를 반대로 이용해서, 회계 장부에 나오는 수치 데이터가 벤포드의 법칙을 따르지 않는다면 조작된 장부가 아닌지 의심해 볼 수도 있습니다.
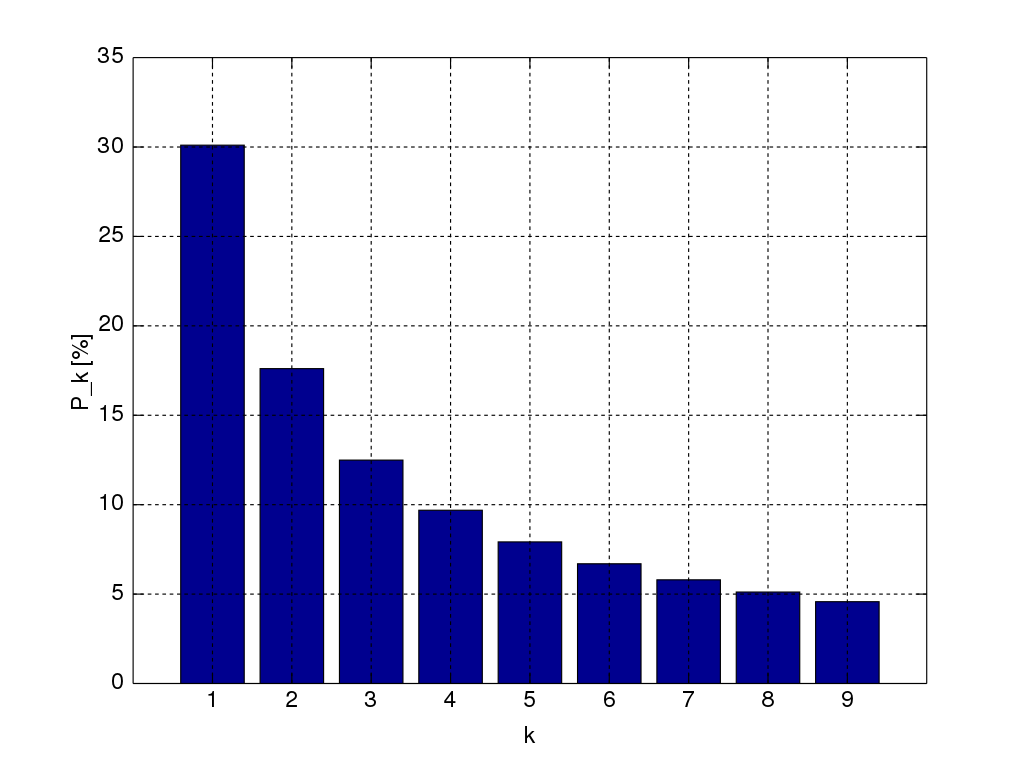
이런 현상이 일어나는 이유가 무엇일까요? 벤포드의 법칙은 수학적으로 잘 정의된 정리가 아니어서 딱 잘라 얘기하긴 어렵습니다. 하지만 대체로 이렇게 생각해 볼 수 있을 것 같습니다. 구독자 수가 100명에서 200명으로 늘어난다는 건 구독자 수가 두 배 증가했음을 의미합니다. 반면 구독자 수가 800명에서 900명으로 늘어난다는 건 12.5% 증가를 의미합니다. 따라서 100명대에선 오래 머물렀어도 800명대에선 비교적 잠깐 머물 가능성이 높습니다. 조금 더 일반적으로 생각해 보자면, 일차함수의 그래프를 그린 뒤 일정한 x 간격으로 점을 찍어 y값 첫째 자리를 확인해 보면 1~9까지의 숫자가 고르게 나오겠지만 지수함수 등의 그래프라면 벤포드의 법칙이 발견될 것입니다.
따라서 구독자 수의 증가가 기존 구독자 수와 독립적으로 일어난다면(즉 일차함수처럼 증가한다면) 벤포드의 법칙이 발견되지 않을 수도 있겠습니다만, 대개는 기존 구독자 수가 구독자 수의 증가 속도에도 영향을 주기 때문에 벤포드의 법칙을 따를 가능성이 높습니다.
덤으로 '1만 시간의 법칙'으로 유명한 맬컴 글래드웰의 책 '아웃라이어'에 나오는, 벤포드의 법칙에 해당하는 사례는 아니지만 벤포드의 법칙과 아주 유사해 보이는 사례를 소개합니다. 캐나다 하키 선수들의 생일은 1~3월에 많이 몰려 있고 12월로 갈 수록 그 비율이 낮아진다는 것입니다. 앞서 벤포드의 법칙이 나타나는 이유를 생각해 보면, 태어난 달은 구독자 수와 같은 종류의 데이터는 아닌 것 같은데 왜 이런 현상이 일어나는 걸까요? 맬컴 글래드웰은 그 이유를 다음과 같이 설명합니다. 캐나다에서는 아주 어린 나이부터 경쟁을 해 가며 하키를 하고, 잘하는 선수들이 추려져 더 많은 훈련을 받고 다음 단계로 올라가게 됩니다. 그런데 어린 나이에는 몇 달 정도의 차이만으로도 성장에서 큰 차이를 보이는 경우가 많고, 캐나다는 1월 1일을 기준으로 선수들의 나이를 나누기 때문에 생일이 빠른 선수들이 어려서부터 계속해서 두각을 나타낼 가능성이 높습니다. 어쩌면 우리는 실제로 재능이 있고 없는 것보다는, 남이 재능을 인정해주느냐 아니냐에 더 많은 영향을 받는지도 모르겠습니다.








의견을 남겨주세요