섀넌의 도깨비 & 켈리 공식: 투자로 돈을 벌 수 있는 수학적인 방법

"계란을 한 바구니에 담지 말라." 전문가들은 분산 투자를 해야 한다고 조언합니다. 하지만 이 조언은 곧잘 오해를 받습니다. 많은 사람들이 위험을 낮추면 그에 비례해서 수익률도 낮아질 거라 생각하기 때문입니다. 당장 저만 해도 투자를 처음 시작할 때, '리스크가 작으면 그만큼 리턴도 작은 게 아닌가. 돈을 벌려면 오를 만한 종목에 집중해서 투자해야지.'라고 생각했습니다(그 덕에 당시 저의 귀여운 계란은 한 바구니 안에서 모조리 박살났습니다.). 분산 투자는, 단순히 하이리스크 하이리턴과 로우리스크 로우리턴을 잇는 직선상에서 적절히 낮은 한 점을 고르라는 조언이 아닙니다. 포트폴리오를 어떻게 구성하느냐에 따라서, 한 종목에 집중했을 때에 비해 수익률은 작게 희생하면서 위험도는 크게 낮추는 것이 가능합니다.

이것을 뒷받침하는 이론이 제임스 토빈에게 노벨 경제학상을 안겨 준 '포트폴리오 이론'인데, 이것에 관해서는 기회가 될 때 별도의 메일에서 다뤄 보겠습니다. 오늘 소개드리고자 하는 내용은 포트폴리오 이론에 앞서, 똑같은 것에 투자하더라도 얼마나 투자하느냐에 따라 수익률이 천차만별로 달라질 수 있음을 보여주는 예시입니다. 섀넌의 도깨비, 그리고 켈리 공식에 대해 알아 보겠습니다.

혹시 AI 서비스인 Claude를 사용해 보신 적이 있나요? 이 서비스의 이름은 천재 수학자 클로드 섀넌에서 따왔습니다. 클로드 섀넌은 손꼽히는 천재 수학자이면서 동시에 여러 다른 분야에도 관심이 많았습니다. 주식 투자에도 상당한 관심과 재능이 있었다고 합니다.

이 섀넌이 강의를 하던 중 재밌는 모델을 제시했습니다. 여기 동전 던지기 게임이 있습니다. 동전을 던져서 앞면이 나오면 1/2 수익을 얻고, 뒷면이 나오면 1/3 손실을 입습니다. 좀 더 몰입하고 싶다면, 주식 시장이라고 해도 좋습니다. 하루는 50% 상승하고 하루는 33% 하락하는 시장입니다.

이 시장에 장기투자를 하면 어떻게 될까요? 만 원을 넣고 장기투자한다면, 하루는 만오천 원으로 올랐다가, 그 다음날엔 만 원으로 돌아오기를 반복하기 때문에 수익은 0입니다.

그렇다면 매일 장이 시작할 때 만 원을 투자했다가 마감할 때 팔고 나온다면 어떻게 될까요? 오르는 날에는 5,000원을 벌고, 떨어지는 날에는 3,333원을 잃기 때문에 평균적으로 하루에 833원을 벌 수 있습니다. 이런 식으로 1년이면 30만 원이 넘는 돈을 벌 수 있습니다. 부럽네요.

정말 재밌는 것은 '매번 재산의 절반을 투자한다'라는 전략으로 임할 때입니다. 처음 재산이 만 원이라면 첫날엔 절반인 5,000원을 투자해서 2,500원을 벌고, 재산은 12,500원이 됩니다. 다음 날에는 12,500원의 절반인 6,250원을 투자해서 2,083원을 손해 보고, 재산은 10,417원이 됩니다. 이틀마다 재산이 4.17% 복리로 늘어나는 셈인데, 이런 식으로 1년 정도 지나면 재산은 1,765만 원으로 불어나 있습니다.

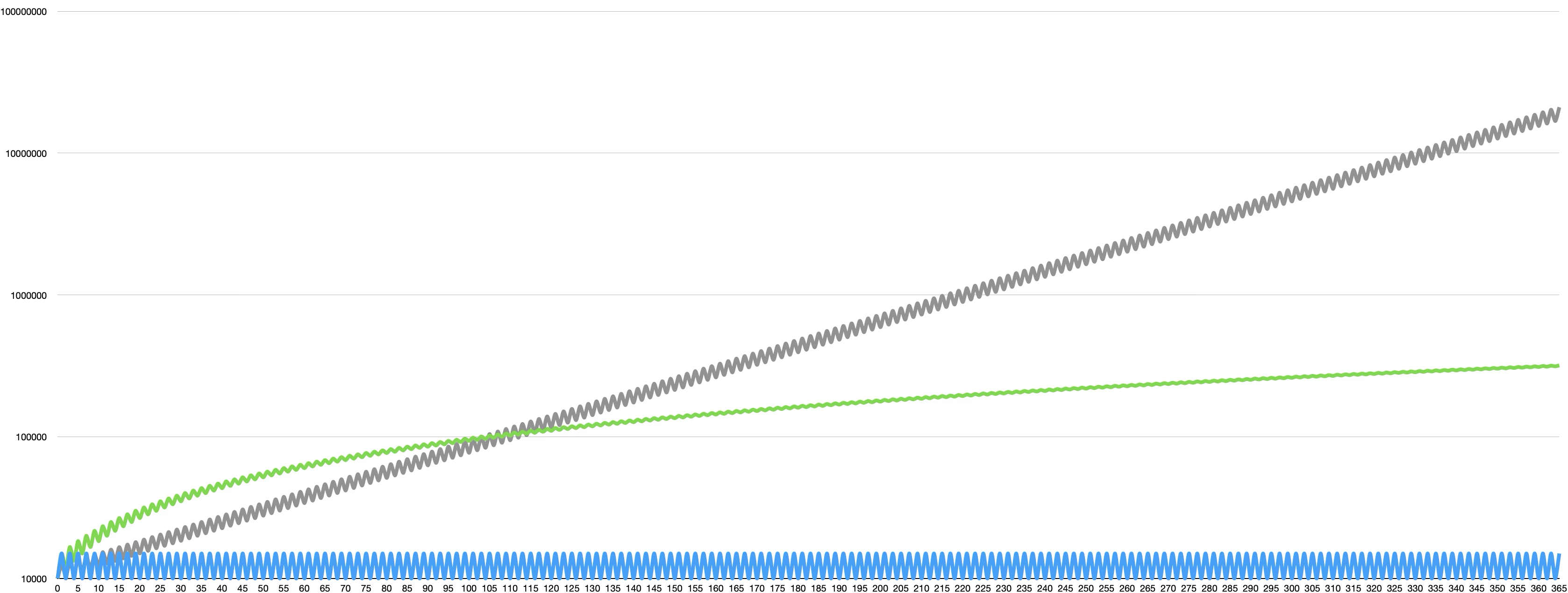
똑같은 시장이었는데 만 원을 1년 간 가만히 넣어 두면 그대로 만 원이 되고, 매일 만 원을 넣었다 빼면 30만 원이 넘는 돈이 되고, 매일 재산의 절반을 넣었다 빼면 1,700만 원이 넘는 돈이 됩니다. 남들보다 나은 종목을 산 것도 아니고 천부적인 감각으로 무릎에서 사서 어깨에서 판 것도 아닌데 이렇게 압도적인 격차를 낼 수 있다는 이 기묘한 현상에 대해 '섀넌의 도깨비'라는 별칭이 붙었습니다.

존 래리 켈리 주니어는 섀넌의 도깨비를 일반화하여 켈리 공식을 만들어냈습니다. 주식시장은 장기적으로 우상향한다는 걸 모두가 알고 있지만 그렇다고 '내가 돈을 벌 수 있다'라는 뜻은 아닌 걸 투자를 해보신 분들은 알고 계실 겁니다. 켈리 공식은 주식시장처럼 이점이 있는 시장에서, 어떻게 투자해야 최고의 수익을 낼 수 있는지 계산하는 공식입니다. 공식은 아주 간단합니다. f = p/a - q/b. f는 우리가 투자해야 하는 비율, p는 수익을 낼 확률, q는 손실을 볼 확률, a는 손실의 크기, b는 수익의 크기입니다. 앞서 섀넌의 도깨비의 경우를 생각해 보면, p = 1/2, q = 1/2, a = 1/3, b= 1/2이 되어 f = 1/2이 나옵니다. 즉 재산의 절반씩을 거는 것이 가장 현명한 전략이라는 의미입니다.

재밌는 실험이 하나 있습니다. 60%의 확률로 앞면이 나오는 동전이 있습니다. 참가자는 이 동전을 던졌을 때 앞면이 나올지, 혹은 뒷면이 나올지에 대해 돈을 걸 수 있고 맞히면 걸었던 만큼의 돈을 추가로 벌고, 틀리면 걸었던 돈을 잃습니다. 참가자들에게 25달러씩을 주고 30분 간 원하는 대로 베팅하게 하자 결과는 다음과 같았습니다. 우선, 참가자의 28%가 파산했습니다. 평균적으로 참가자들은 91달러 밖에 벌지 못했습니다. 30%의 참가자는 '올인'을 시도했습니다. 참가자 중 2/3는 뒷면에 베팅하기도 했습니다. 사기 동전을 줘도 이렇게 돈을 못 번다니 답답하지만, 비웃기에는 남 얘기 같지가 않습니다. 분명 앞면이 60%라고 했는데 이상하게 내 동전은 뒷면이 더 잘 나오는 것 같아서 뒷면에 걸기도 하고, '에라 모르겠다, 인생 한 방이지'라는 마음으로 올인을 해보기도 하는 게 흔한 투자자의 모습입니다.

하지만 우리는 이제 켈리 공식을 알고 있기 때문에 적절한 투자 전략을 짤 수 있습니다. p = 3/5(앞면이 나올 확률 60%. 당연히 앞면에 걸어야 한다는 건 더 설명하지 않겠습니다.), q = 2/5(뒷면이 나올 확률 40%), a = 1(틀리면 모두 잃으므로), b = 1(맞히면 건만큼 벌므로)이기 때문에 켈리 공식에 따라 f = 1/5이 됩니다. 즉 매번 가진 돈의 20%를 걸면 됩니다. 처음 주어진 돈이 25달러이므로 첫번째에는 앞면에 5달러를 걸면 되겠습니다. 100번 정도 베팅하면 187달러로 불어나 있을 것입니다.

그동안 보낸 페퍼노트가 총 160편입니다. 이 중에 알아 둔다고 밥 먹여 주는 지식은 아마 없지 않았나 생각합니다. 소에게 자석을 먹이는 이유라든지, 울릉도 호박엿이 원래는 호박으로 만드는 게 아니라는 걸 알아봐야 삶에 큰 도움은 안 됐을 것입니다. 이번 페퍼노트가 최초로 돈 버는 데 도움이 되는 내용 같은데, 아무쪼록 구독자 분들 모두 부자 되시길 기원해 보겠습니다.

더 알아보기

문병로 교수의 메트릭 스튜디오
나무위키, 포트폴리오 이론
나무위키, 분산투자#원리 - 섀넌의 도깨비
Wikipedia, Kelly criterion