전에 '루퍼트 왕자의 눈물'이라는 멋진 이름을 가진 물건을 소개해 드린 적이 있습니다. 이 '루퍼트 왕자(Prince Rupert of the Rhine)'라는 인물을 페퍼노트에서 한 번 더 소개할 일이 있을 줄은 몰랐는데, 이 분이 수학계에도 이름을 남긴 게 있었습니다.
여기 똑같은 크기의 주사위 2개가 있습니다. 한 주사위에 구멍을 냅니다. 단 주사위가 쪼개져 버리지는 않게 조심해야 합니다. 구멍을 잘 뚫으면, 다른 주사위가 이 주사위의 구멍으로 통과할 수 있을까요?
제 생각엔 어찌어찌 비스듬하게 잘 뚫으면 통과할 수 있을 것 같습니다. 호기심 많은 루퍼트 왕자도 그렇게 생각했는지 이 문제에 대해 내기를 걸었습니다. 그리고 당대 영국의 수학자 존 월리스(John Wallis)가 실제로 가능하다는 것을 증명해 냈습니다. 그는 정육면체의 공간 대각선(한 꼭짓점에서 정반대편 꼭짓점으로 가는 선)에 평행하게 구멍을 뚫으면, 똑같은 크기의 정육면체는 물론이고 약 1.035배 큰 정육면체까지도 통과할 수 있음을 밝혔습니다. 약 100년 뒤에는 네덜란드의 수학자 피터 니우란트(Pieter Nieuwland)가 구멍을 뚫는 각도를 적절히 조정하면 약 6% 더 큰 정육면체까지도 통과시킬 수 있음을 증명했습니다.

수학자들은 이런 성질을 '루퍼트 성질(Rupert property)'이라고 부르기로 했습니다. 어떤 입체 도형이 자기 자신과 같거나 더 큰 복사본을 자신을 뚫고 통과시킬 수 있다면, 그 도형은 루퍼트 성질을 가진다고 말합니다.
수학자들은 이런 문제를 푸는 것만으로는 꼭 만족하지 못하고 다음 질문을 이어갑니다. "그렇다면 다른 다면체는 루퍼트 성질을 갖고 있을까?" 노력 끝에 정육면체 외에도 정사면체, 정팔면체, 정십이면체, 정이십면체, 그리고 온갖 다른 다면체에서도 루퍼트 성질이 발견되었습니다.
이제 수학자들은 그 다음 단계의 궁금증을 갖습니다. "혹시 모든 볼록다면체가 루퍼트 성질을 가지는 게 아닐까?" 딱히 반례가 나오는 건 없었고, 어떤 볼록다면체든 비스듬하게 잘 뚫으면 자기 자신을 통과시킬 수 있어 보였습니다.
하지만 바로 2025년 올해, 야콥 슈타이닝거(Jakob Steininger)와 세르게이 유르케비치(Sergey Yurkevich)가 루퍼트 성질을 갖지 않는 최초의 볼록 다면체를 발견했습니다. 이 도형은 '노퍼트헤드론(Noperthedron)'이라는 이름을 얻었습니다. 'no'와 'Rupert'를 합친 말로, "루퍼트 성질이 없다"는 뜻입니다.
노퍼트헤드론은 90개의 꼭짓점, 240개의 모서리, 152개의 면(삼각형 150개와 정15각형 2개)을 가진 도형입니다. 이렇게 말만 들으면 굉장히 이상하게 구겨진 모양이 아닐까 싶은데 막상 보면 그렇게 특이하게 생기지는 않았습니다.
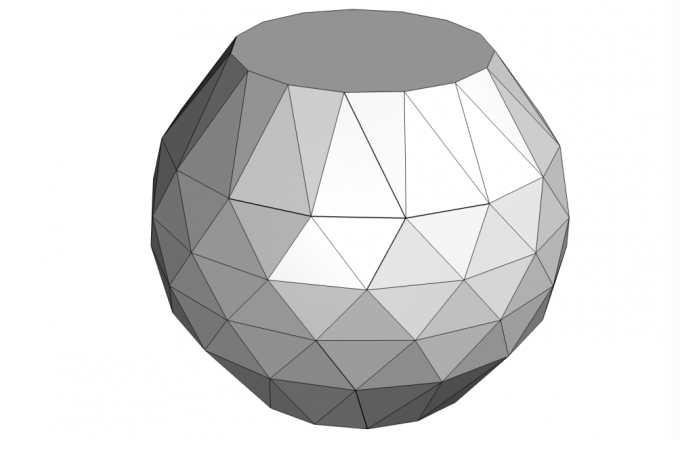
연구자들은 이 도형에 뚫을 수 있는 방향들을 1800만 개의 작은 블록으로 나누어서 검토했고, 그 어떤 방법으로도 같은 크기의 노퍼트헤드론을 통과시킬 수 없다는 것을 증명했습니다. 검증만 30시간이 걸리는 2.5GB 크기의 증명이었습니다.
수학자들의 궁금증은 또 멈추지 않습니다. 4차원 초입방체(tesseract), 5차원, 6차원 등 시각적으로 상상하기도 힘든 차원에서는 어떨까요? 놀랍게도 n차원 초입방체는 모든 차원에서 루퍼트 성질을 가진다는 것이 증명되었습니다. 3차원 주사위 뿐 아니라 4차원, 5차원, 6차원의 주사위에도 모두 자신과 같은 크기의 주사위를 통과하는 구멍을 뚫을 수 있습니다.
그 다음 단계의 궁금증은 또 어떤 게 있을 수 있을까요? 루퍼트 왕자의 작은 내기는 많은 이들의 호기심을 타고 어디까지 뻗어나갈 수 있을까요?
더 알아보기
페퍼노트, 총으로도 깰 수 없지만 톡 쳐서 깰 수도 있는 유리, 루퍼트 왕자의 눈물과 볼로냐 병
페퍼노트, 수학은 항상 아름답기만 하진 않습니다
페퍼노트, 이 세계가 4차원이냐고요? 그렇기도 하고 아니기도 하죠.








의견을 남겨주세요