벌써 3개월 전이 된 '초등학생도 이해할 수 있지만 아무도 풀지 못한 수학 문제' 메일을 기억하시나요? '콜라츠 추측'이라는 난제를 소개한 글이었습니다. 오늘은 콜라츠 추측만큼 이해하기 쉬우면서, 아직 답이 나오진 않았고, 아주 귀여운 이름이 붙어 있는 난제를 가져 왔습니다. Moving Sofa Problem, 소파 옮기기 문제입니다.

이사를 해보신 분이라면 좁은 문이나 복도로 소파, 책상 같은 가구를 통과시키느라 고생하신 경험이 있으실 겁니다. 소파 옮기기 문제는 이런 상황을 수학적으로 재밌게 만든 문제입니다. 복도의 길이와 높이는 고려하지 않고, 폭이 1이고 직각으로 꺾여 있는 복도를 통과할 수 있는 소파 중, 가장 면적이 큰 소파가 무엇인지 찾는 게 목표입니다.
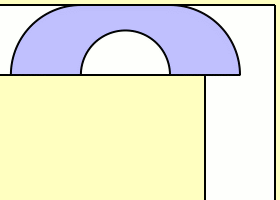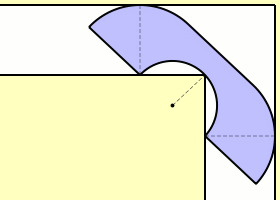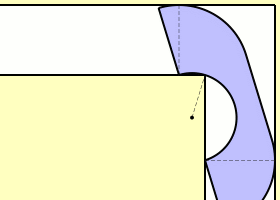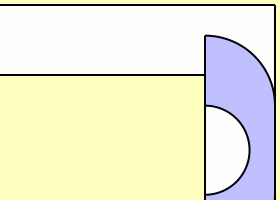
예를 들어 위 이미지의 '해머슬리 소파'는 복도의 폭에 딱 맞게 겨우겨우 돌아 들어가는 것을 확인할 수 있습니다. 이 때의 넓이는 약 2.2074입니다(복도의 폭을 1로 합니다.). 해머슬리 소파를 발견한 해머슬리는 소파가 아무리 커도 2√ 2, 약 2.8284보다 클 수 없음(이걸 상계라고 합니다.)도 증명했습니다. 현재까지 발견된 가장 넓은 소파는 해머슬리 소파와 비슷하게 생긴 '게르버 소파'로 약 2.2195의 넓이를 갖고 있습니다.

2017년에는 상계도 해머슬리가 증명했던 값보다 한참 작은 2.37까지 증명이 되었습니다. 즉 여러분에게는 2.2195와 2.37 사이의 기회가 남아 있는 셈입니다. 게르버 소파보다 더 큰 소파를 찾아내시거나, 게르버 소파가 가능한 최대 크기의 소파임을 증명해 내신다면 세계 최초라는 업적 하나를 세우실 수 있습니다. 오늘 한 번 거실 소파를 여기저기 옮겨 보시는 건 어떠신가요?








의견을 남겨주세요
ㅇㅇ
PIVOT!!!!!!!!!!!!!!!!!!!!!!!
의견을 남겨주세요
빔일
추억의 에피소드 ㅎ
의견을 남겨주세요
페퍼노트
게르버 소파가 가능한 최대 크기의 소파임을, 한국의 백진언 박사님이 증명해 냈습니다. 페퍼노트에서 아직 해결되지 않았다 소개드렸던 문제가 한국인에 의해 해결이 되었다는 점이 놀랍고 자랑스럽습니다. https://www.quantamagazine.org/the-largest-sofa-you-can-move-around-a-corner-20250214/ https://www.youtube.com/watch?v=3ONcYbhJaUg
의견을 남겨주세요