외야수가 공을 잡는 법, 매가 오리를 잡는 법, 전투기가 폭격기를 잡는 법

야구 경기에서 외야수가 뜬공을 잡는 모습을 본 적이 있으신가요(네? 우리 팀 외야수는 잡는 꼴을 못 봤다고요?)? 제가 직접 계산을 해본 건 아니지만 공이 떨어질 위치는 아마 타자가 공을 때린 직후 거의 결정되어 있을 것입니다. 공이 날아온 속도, 배트와 공이 맞은 각도, 배트가 가한 힘, 공에 걸려 있는 회전, 불고 있는 바람 등 여러가지 변수를 정확히 알고 있다면 공을 보지 않아도 공이 어디에 떨어질지 알 수 있을 것입니다. 배트가 공을 때린 순간 이를 계산해 그곳으로 반듯이 달려가면 공을 잡을 수 있습니다.

하지만 실제로 외야수가 그렇게 하지는 않습니다(우리 팀 외야수가 이번엔 공을 잡았다고 하더라도요.). 외야수는 계속 공을 쳐다보면서 달려갑니다. 외야수는 본능적으로, 공을 향한 시선의 각도가 유지되도록 달려갑니다.

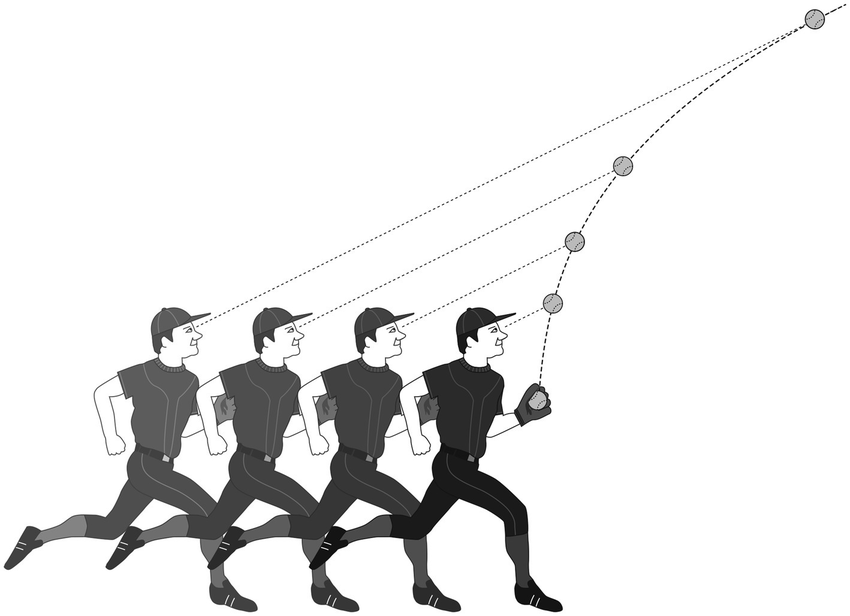
이 과정에서 외야수가 움직이는 경로는 직선이 아니라 구불구불한 곡선이 되기도 합니다. 이동경로만 보면 비효율적이라 할 수 있지만 실제로는 대단히 효율적인 방법입니다. 타자가 공을 칠 때마다 복잡한 방정식을 풀고 있어야 한다면, 직선으로 달려간대도 이미 타자는 홈에 들어왔을 테니까요(어차피 못 잡을 거 방정식이라도 좀 풀어보라고요?).

인간만 이런 방법을 사용하는 게 아닙니다. 매가 오리를 사냥할 때도 똑같은 방법을 씁니다. 매는 오리가 어디로 날아갈지 미리 계산하지 않습니다. 그냥 오리를 바라보는 각도를 유지하며 쫓아갑니다.

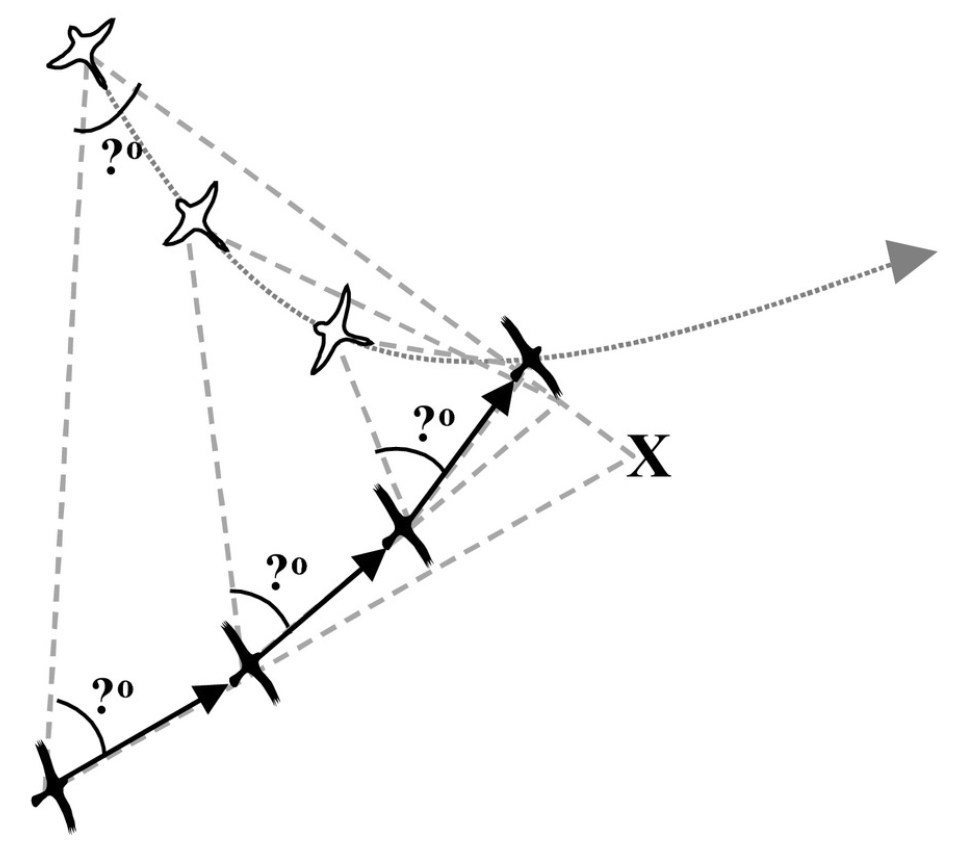
이렇게 바라보는 각도를 일정하게 유지하며 쫓아가는 방법을 '시선 휴리스틱(Gaze heuristic)'이라 합니다. 매도, 외야수도, 본능적으로 행하는 방법이지만 군사적으로도 큰 힘을 발휘합니다.

제2차 세계대전이 시작되기 전, 영국 공군은 전투기로 적군 폭격기를 요격할 알고리즘을 연구하고 있었습니다. 여러 수학자, 과학자들이 모여 해결책을 찾으려 했습니다. 온갖 수식이 동원됐지만 날아가는 비행기를 비행기로 잡아낸다는 것은 쉬운 일이 아니었습니다. 목표로 잡은 요격률 90%는 요원했습니다.

이런 상황 속에서 영국 공군 기지 사령관 E.O. 그렌펠이 나섰습니다. "이럴 바에 그냥 제가 눈으로 보고 지시하면 안 됩니까?" 워낙 상황이 안 풀리고 있었다 보니 그렌펠에게도 기회가 주어졌습니다.

결과는 놀라웠습니다. 복잡한 계산들로는 하지 못했던 일을 그렌펠의 눈은 해냈습니다. 그가 90%의 정확도로 요격을 해내자 그의 '감'에 대한 연구가 이뤄졌습니다. 그의 방법은 간단했습니다. 야구선수가 뜬공을 잡듯이, 매가 오리를 사냥하듯이, 그냥 일정한 각도를 유지하며 전투기를 폭격기 쪽으로 보낸 것이었습니다.

이 비법 덕에 2차 대전이 벌어졌을 때 연합군은 독일군보다 안 좋은 성능의 레이더를 달고도 유리한 입장에서 공중전을 치를 수 있었습니다.

전쟁이 끝난 후 미국은, 독일의 미사일 기술과 영국의 간단한 요격 비법을 응용해 유도 미사일을 만들었습니다. 당시 그들의 목표는 '세탁기보다 복잡하지 않은' 유도 미사일을 만드는 것이었습니다. 시선 휴리스틱은 이런 단순하고도 효율적인 설계에 제격이었습니다. 이렇게 탄생한 사이드와인더(Sidewinder)라는 이름의 미사일은 지금도 대표적인 단거리 공대공 미사일로 사용되고 있습니다.

우리는 선입견, 편향 같은 말을 흔히 안 좋은 의미로만 사용합니다. 대충 감으로 때려 맞히는 것은 어설픈 것으로 취급합니다. 하지만 시선 휴리스틱 덕분에 야구 선수는 물리학 공식을 몰라도 뜬공을 잡고, 매는 수학을 몰라도 사냥에 성공하고, 그렌펠은 복잡한 계산 없이도 폭격기를 잡아냈습니다.

어려운 문제에 봉착했을 때 혹시 너무 복잡하게 생각하고 있는 건 아닌지 돌아보세요. 때로는 매의 본능이 전문 지식보다 유용할 수도 있습니다.

더 알아보기

Robert P. Hamlin, "The Gaze Heuristic": Biography of an Adaptively Rational Decision Process
Gerd Gigerenzer, Henry Brighton, Homo Heuristicus: Why Biased Minds Make Better Inferences
톰 치버스, 모든 것은 예측 가능하다