네 명이 오리라...

제가 초등학생일 때에 유행했던 '버디버디' 같은 메신저나 '큐플레이' 같은 게임에서는 '~~악마(주로 앙마라고 쓰는 게 트렌드였습니다.)'라는 닉네임이 많았습니다. 악마가 주는 어딘가 나빠 보이고 삐뚤어져 보이는 느낌이 오히려 쿨해 보였던 게 아닌가 싶습니다. 영단어로도 Badass라 하면 멋있는 걸 뜻하는 것처럼요. 솔로몬의 72 악마 같은 것은 뭔지 몰라도 이름만으로도 멋지게 느껴지지 않나요?

과학계(특히 물리학계)에는 참 멋있는 용어가 많아서 수학을 전공한 저로서는 부럽기도 합니다. 오늘은 과학계의 멋있는 용어들 중에서도 '악마'라는 이름을 가진 네 개념을 알아 보겠습니다.

라플라스의 악마

이공계 전공자 분들께는 '라플라스 변환' 등으로 익숙할 라플라스는 우주에 있는 모든 원자의 정확한 위치와 운동량을 알고 있는 존재가 있다면 뉴턴의 운동 법칙을 이용해 과거, 현재의 모든 현상을 설명하고 미래까지 예언할 수 있다고 했습니다. 멋있는 용어가 넘치는 물리학계답게, 후에 이러한 능력을 지닌 존재를 가정한 것에 '라플라스의 악마'라는 이름이 붙습니다.

쉽게 말하자면 이 세상 모든 데이터를 갖고 있으면 모든 것을 예측할 수 있다는 것인데, 현대에는 라플라스의 악마 같은 존재가 있을 수 없음이 잘 알려져 있습니다. 불확정성 원리에 의해 원자의 위치와 운동량을 동시에 정확히 알 수 없기 때문입니다.

맥스웰의 악마

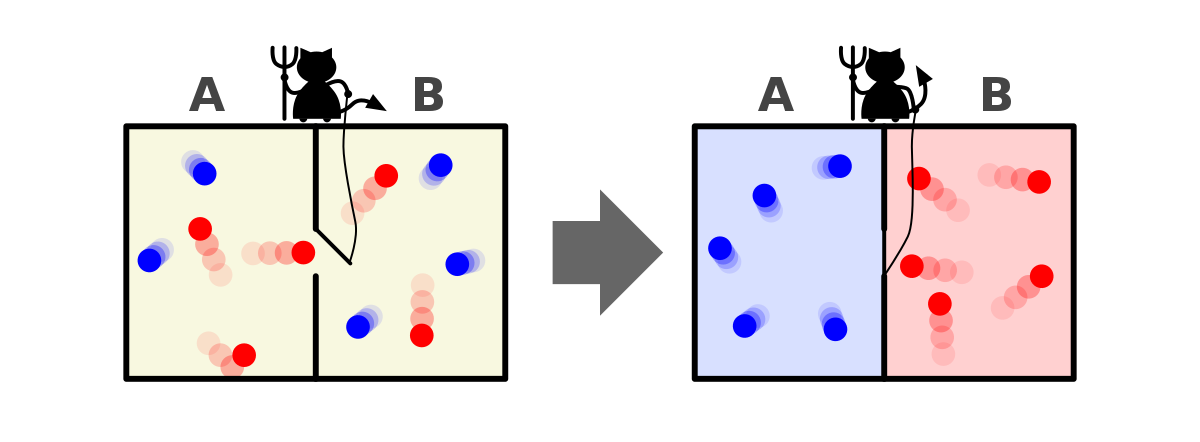
맥스웰의 악마는 전자기학을 정립한 역사 상 가장 위대한 물리학자 중 한 명인 제임스 클러크 맥스웰이 고안한 사고실험에 등장하는 악마입니다. 방 안에 두 종류의 기체가 가득 차 있고 그 방 가운데에 벽이 있습니다. 그리고 이 벽에는 문이 있습니다. 악마의 목표는 두 기체를 벽 좌우로 분리하는 것입니다. 악마는 절대로 직접 기체 분자를 건드리지는 않습니다. 악마는 엄청난 동체시력과 반사신경을 가지고 있어서 문 쪽으로 기체 분자가 다가오면 기체의 종류를 확인하고 목표에 맞게 문을 열거나 닫습니다. 이것을 오랫동안 반복하면 섞여 있던 기체가 둘로 분리되게 됩니다.

이것은 '고립계의 엔트로피는 감소하지 않는다'라는 내용의 열역학 제2법칙을 위배하는 결과입니다. 열역학 제2법칙에 따르면 기체 분자를 누군가 직접 건드리지 않는다면 분리되어 있던 기체가 섞여 나가는 쪽으로 움직여야지 그 반대로 움직일 수는 없습니다. 그런데 맥스웰의 악마는 기체 분자를 직접 건드리지는 않고 적당히 문을 열고 닫는 것으로 기체를 분리시켰습니다. 모순이 발생한 것입니다.

이 역시 라플라스의 악마처럼 현대 과학에서 충분히 설명이 됩니다. 맥스웰의 악마가 문에 다가오는 기체 분자가 어떤 분자인지, 언제 문을 열고 닫아야 이 분자를 오가게 할 수 있을지 판단하려면 이 분자를 관측해야 합니다. 그리고 관측이라는 행위가 곧 기체 분자를 건드려야만 할 수 있는 행위라는 것이 지금의 과학의 설명입니다. 따라서 악마가 정보를 얻고 처리하는 것까지도 엔트로피 계산에 포함되어야 하며, 이럴 경우 방 안의 엔트로피는 감소하지 않습니다.

데카르트의 악마

르네 데카르트의 사고실험에 등장하는 악마입니다. '통 속의 뇌'라는 개념에 대해 들어 보셨나요? 우리가 만약 실험실에 있는 유리 통 속의 뇌인데 이 뇌에 전극을 꽂아서 우리가 이 세상을 느끼고 있는 것처럼 만든다면, 우리는 이 세상이 진짜인지 전기 신호로 만들어진 가짜인지 구분할 수 있을까요? 데카르트의 악마가 정확히 이와 같은 행동을 합니다. 우리의 모든 감각기관에 환상을 보여주고 들려주는 것입니다.

그리고 데카르트의 악마가 아무리 거짓 정보를 주어도 이 거짓 정보에 속고 있는 나라는 존재는 부정할 수 없다는 게 데카르트의 생각이었습니다. 그렇게 나온 말이 바로 그 유명한 '나는 생각한다. 고로 존재한다.'입니다.

다윈의 악마

진화론으로 유명한 찰스 다윈의 이름이 붙은 악마입니다. 다윈의 이름이 붙은 이유는, 모든 생물학적 제약에서 벗어나 자연선택적 적합성을 극대화한 생물을 가정한 개념이기 때문입니다. 다윈의 악마는 출생하자마자부터 번식이 가능하고 그 수명은 영원하며 천적은 없습니다. 이 생물은 제약 없이 무한정 번식해 나갈 수 있습니다. 이런 생물은 실제로 존재하진 않습니다만 생물학자들은 생물들의 생존 전략이나 진화적 균형에 관한 사고 실험을 할 때 이 개념을 사용합니다.